|
Leonardo's vitruvian man
Leonardo di ser Piero da Vinci (1452�1519) had drawn the vitruvian man
comming from the architect Vitruvius (Marcus Vitruvius Pollio, around the first century).
The body standing is inscribed in a square.
With feet and arms outspread, the man is inscribed in a circle.
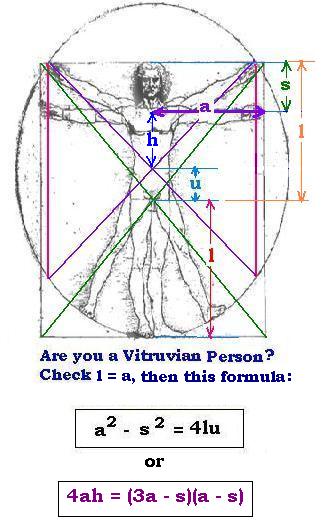
Calculations:
Using the square:
HD = diagonal/2
HD2 + HD2 = 2 HD2 = (2a)2
Hence:
HD2 = 2a2
HD2 = l2 + a2
Then:
l2 + a2 = 2a2
Hence:
l = a
Using the circle:
s2 - a2 = r2 - (l - u)2
where r is the radius of the circle.
r = l + u, then:
a2 - s2 = (l + u)2 - (l - u)2
= (l + u + l - u) x (l + u - l + u) = 2 l x 2 u = 4 ul
Hence:
a2 - s2 = 4 ul
with l = a, we have:
a2 - s2 = 4 ua
We have also:
h = l - u - s ( or a - u - s)
u = l - s - h = a - s - h
The above formula becomes:
(a + s)(a - s) = 4 a (a - s - h)
(a + s)(a - s) - 4 a (a - s - h) = 0
(a + s)(a - s) - 4 a (a - s) + 4ah = 0
4 a (a - s) - (a + s)(a - s) = 4ah
4ah = (3a - s)(a - s)
4ah = (3a - s)(a - s)
|