|
|
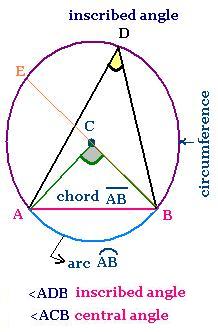
1. definitions
The inscribed angle <ADB and the central angle
<ACB intercept the same arc AB.
We have CA = CB = radius of the cercle of center C
which is equal to the half of the diameter BE.
The circumference measures 2π x radius = π x diameter.
A sector is the area delimited by two radii and an arc lying between
these two radii, is. A segment is the area delimited by a chord and
an arc.
How to define a radian?
By definition, one radian is the measure of a unit plane angle,
equal to the central angle of a circle intercepting an arc equal in length
to the radius.
The circumference "C" of a circle of radius "R" measures 2πR. We have
then 2πR/R = 2π = 8.28 arcs meausuring R in the circumference 2πR.
If 180 degrees corresponds to π radian, one radian = 180/π = 57.29 degrees.
We write 1 rad = 57.29o.
The rad is used under the SI (Systeme International d'Unites) unit.
|
2. Inscribed angles
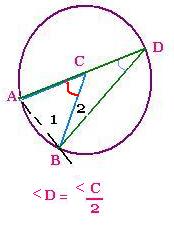
2.1 First case: One
side of the inscribed angle is a diameter of the circle:
CD = CB, because both are radii of the cercle. Then
<BCD is an isosceles triange. The angle <B2 and <D
are then equals. <B2 = <D.
We can write:
(180 - <C) + <B2 + <D = 180
Then:
<D = <C/2
An inscribed angle is the half of the
central angle, when they both intercept the same arc.
|
|
|
| |
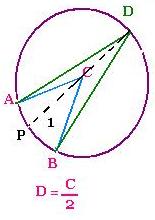
2.2 Second case:
The central angle is inside the inscribed angle:
Draw the chord DP that passes by the center of the circle "C"; we
have:
Angle <D = <ADB = <ADP + <BDP = <ACP/2 + <BCP/2
= <ACB/2. Then
<D = <C/2
An inscribed angle is the half of the
central angle, when they both intercept the same arc.
|
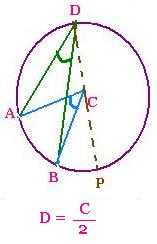
2.3 Third case:
The central angle is ouside the inscribed angle:
Draw the diameter DP, we have:
Angle <D = <ADB = <ADP - <BDP = <ACP/2 - <BCP/2 =
<ACB/2 <C/2
Then:
<D = <C/2
An inscribed angle is the half of the
central angle, when they both intercept the same arc.
|
|
|
|
|
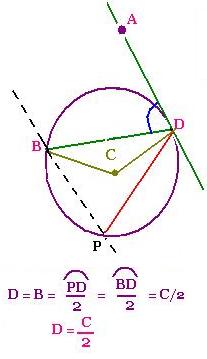
2.4 Fourth case:
The limit case where the inscribed angle is
formed by a chord and a tangent:
Draw a parallel BP to DA; we have:
Angle <D = Angle <B.
The angle <B is an inscribed angle that intercepts the arc PD
which is equal to to the arc BD (because AD and BP are parallel).
Then:
<D = <C/2
An inscribed angle is the half of the
central angle, when they both intercept the same arc; even
in the limit case where the inscribed angle is formed
by a tangent and a chord.
|
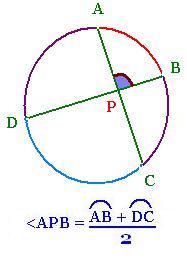
3. Two intersecting chords:
Draw two chords AC and DB in the circle; we
have:
Angle <APB + Angle <BPC = 180
<BPC = 180 - (<CBP + <PCB) =
180 - (arc DC/2 + arc AB)
Then:
<APB = 180 - <BPC = 180 - 180 + arc DC/2 + arc AB/2
<APB = (arc DC+ arc AB)/2
<APB = (arc DC + arc AB)/2
| |
|
|
|
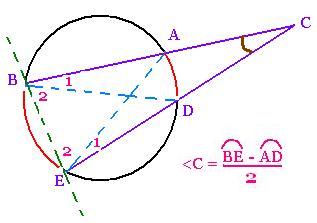
4. Angle of two secants:
Draw two secants BC and EC; we have:
Angle <EAB = Angle <BDE = Arc BE /2. Then:
<BDC = <EAC
<C + <B1 + <B2 + <E1 + <E2 = 180
<C + <B1 + <E1 + <B2 + <E2 = 180
<C + arc AD/2 + arc AD/2 = 180 - (<E2 + <B2)
We have:
<E2 + <B2 = arc ED/2 + arc AB/2
And, for the whole circumference:
(arc AB + arc BE + arc ED + arc DA)/2 = 180
Then:
<C = (arc AB + arc BE + arc ED + arc DA)/2 - arc AD - arc ED/2 - arc AB/2
<C = arc BE/2 - arc AD/2
<C = (arc BE - arc AD)/2
|
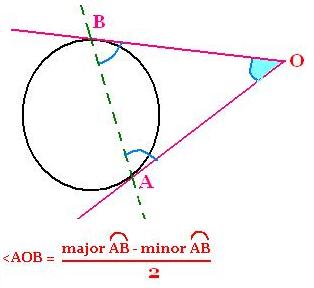
5. Two tangents:
Draw two tangents AO and BO; we
have:
Angle <BAO = minor arc AB/2 = <ABO
<BAO + <ABO = 2 <BAO = 180 - minor arc AB.
We have for the whole circumference:
180 = (major arc AB + minor arc AB)/2
Then:
<AOB = 180 - 2 <BAO = (major arc AB + minor arc AB)/2 - minor AB
= (major arc AB - minor arc AB)/2
<AOB = (major AB - minor AB)/2
| |
|
|
|
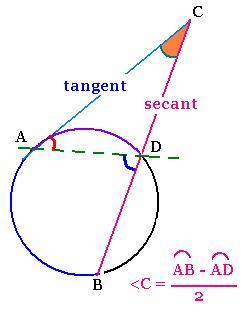
6. Tangent and secant :
Draw a secants BC and a tangent AC; we have:
Angle <A = Arc AD /2. Then:
<C + <A = <D = arc AB/2. So
<C = arc AB/2 - <A = arc AB/2 - arc AD/2
<C = (arc AB - arc AD)/2
<C = (arc AB - arc AD)/2
|
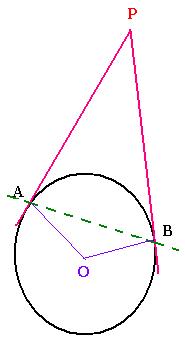
7. Two secants
The two angles PAB and PBA intercept the same arc AB/2 (they
are formed by the chord AB and a tangent). Then, the triangle
PAB is isosceles. Furthermore PA = PB.
The two segments drawn from an exterior point of
a circle and tangent to this circle are equal in length.
According to the sine law, if two angles of a triangle
are congruent, their opposite sizes are also congruent, then
the triangle is isosceles.
AP/sinB = PB/sinA. If angle A = angle B, then AP = BP, and
the triangle APB is isosceles.
| |
|
axiom
theorem
postulate
Lemma
corollary
© The Scientific Sentence. 2007.
| |
|









