Contents
Special Relativity
© The scientific sentence. 2010
| Relativity: The 4-Vectors
1. Lorentz Transformations
From the reference frame at rest (RF):
The velocity of the reference frame (RF) is 0
The velocity of the moving reference frame (MF) is v
The velocity of the moving object is u.
From the moving frame (MF):
The velocity of the moving reference frame (MF) is 0
The velocity of the reference frame (RF) is - v
The velocity of the moving object is u'
In the (MF):
Galilean transformations give:
t' = t
x' = x - vt
y' = y
z' = z
and
Lorentz Transformations give:
t' = γ(t - vx/c2)
x' = γ(x - vt)
y' = y
z' = z
where
γ = 1/[1 - β2]1/2, and
β = v/c
We have also the reverse transformation:
t = γ(t' + vx'/c2)
x = γ(x' + vt')
y = y'
z = z'
2. Proper time
If an object is at rest in the mooving reference
frame u' = 0. So its velocity in the (RF) is v, because the
velocity of the (MF) is v in the (RF).
In the (RF):
If the object starts to move at t = 0 along the
x-axis. At a time later t, the object is located at:
x = vt, y = 0, z = 0, t = t
In the (MF):
The object is located at:
x' = γ(vt - vt) = 0
y' = y
z' = z
t' = γ(t - v vt /c2) =
γ t (1 - (v /c)2) =
γ t (1/γ2) = t/γ
In the (RF): time = t, and
In the (MF): time = t' = t/γ < t
In the (RF) t = γ t' : The time is dilated.
t' is the proper time, which measures
time in the moving reference frame.
3. 4-Vectors notations
For an event E = (t, x, y, z), Lorentz transformation
is then an operator that transforms this 4-Vector
on another 4-Vector event E' = (t', x', y', z') =
(γ(t - vx/c2), γ(x - vt), y, z) within
a certain vector space called the Minkowski space, which
is a 4-Dimension Cartesian space with a specific property
of the inner product.
But, in order to have the same dimension, that is a length,
for all of the 4 components, we just make following change in
Lorentz transformations, and get:
ct' = γ(ct - vxc/c2)
x' = γ(x - vtc/c)
y' = y
z' = z
That is:
ct' = γ(ct - βx)
x' = γ(x - β ct)
y' = y
z' = z
And have instead:
E = (ct, x, y, z), transformed in:
E' = (ct', x', y', z') = (γ(ct - βx), γ(x - β ct), y, z)
4. The invariant (Δs)2 = - c2t2 + r2
In the (MF):
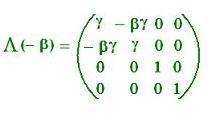
The event E = (ct, x, y, z), transformed into the event:
E' = (ct', x', y', z') = (γ(ct - βx), γ(x - β ct), y, z),
ct' = γ(ct - βx)
x' = γ(x - β ct)
y' = y
z' = z
Therefore
E' = Λ(- β) E
In the (RF):
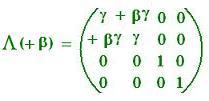
The event E' = (ct', x', y', z'), is transformed in the event:
E = (ct, x, y, z) = (γ(ct' + βx'), γ(x' + βct'), y', z')
ct = γ(ct' + βx')
x = γ(x' + β ct')
y = y'
z = z'
Therefore
E = Λ(+β) E'
That we can write:
c(-t') = γ(c(-t') - βx')
x = γ(x' - β c (-t'))
y = y'
z = z'
So, in the (MF):
The event E' = (-ct', x', y', z'), is transformed in the event:
E = (-ct, x, y, z) = (γ(-ct' - βx'), γ(x' - βct'), y', z')
Therefore
E = Λ(-β) E'
That is:
If E is tranformed with Λ(-β) in E', E' is tranforme
with Λ(+β) in E. Thus, to transform E' in E with
Λ(-β), we have to change the time t' into -t'. That is
we replace (ct, x, y, z) = Λ(+β) (ct', x', y', z') by
(-ct, x, y, z) = Λ(- β) (-ct', x', y', z')
Hence:
(ct', x', y', z') = Λ(-β) (ct, x, y, z)
(-ct, x, y, z) = Λ(- β) (-ct', x', y', z')
or
(ct, x, y, z) = Λ- 1(ct', x', y', z')
(-ct, x, y, z) = Λ(- β) (-ct', x', y', z')
The scalar product gives:
(ct, x, y, z) . (-ct, x, y, z) = Λ- 1(ct', x', y', z') . Λ(- β) (-ct', x', y', z') = (ct', x', y', z') (-ct', x', y', z')
or
(ct, x, y, z) . (-ct, x, y, z) = (ct', x', y', z') (-ct', x', y', z')
That is
- c2t2 + x2 + y2 + z2 =
- c2t'2 + x'2 + y'2 + z'2
Therefore, if the vector space r has the components x, y , and z:
Under Lorentz transormations, the squared norm of an event is constant:
The squared distance: - c2t2 + x2 + y2 + z2
= - c2t2 + r2 is an invariant .
(Δs)2 = - c2t2 + r2 is invariant .
5. Covariance and contravariance Notations
We will use the following notation:
For the kind of 4-Vector: (ct, x, y, z):
(ct, x, y, z)
= (x0, x1, x2, x3) or xμ for short, μ = 0, 1, 2, 3.
xμ is called contravariant 4-vector.
For the kind of 4-Vector: (- ct, x, y, z):
(- ct, x, y, z)
= (x0, x1, x2, x3) or xμ for short, μ = 0, 1, 2, 3.
xμ is called covariant 4-vector.
So
(Δs)2 = xμ . xμ
= Σ xμ xμ
μ = 0, 1, 2, 3.
= x0x0 + x1x1 + x2x2 + x3x3
The fact that to use xμ for short, leads to following notation called
Einstein notation:
Σ xμ xμ = xμ xμ
μ = 0, 1, 2, 3.
Let's find again that the defined scalar product is invariant:
(a0, a) = aμ un event, Lorentz-transformed into
(a'0, a') = a'μ, and
(b0, b) = bμ un event, Lorentz-transformed into
(b'0, b') = b'μ
Remark that
bμ = (b0, b) = (- b0, b)
a'μb'μ = (a'0, a')(b'0, b')
= - γ(a0 - βa1)γ(b0 - βb1) +
γ(a1 - β a0)γ(b1 - β b0) +
a2b2 + a3b3 =
γ2[
- a0b0 +
βa1b0
βa0b1
+ βb1a0 - βb1βa1
+ a1b1
- β a0b1
- β b0a1 +
β b0β a0]
+ a2b2 + a3b3
=
γ2[
(a0b0 - a1b1) (β2 - 1)]
a2b2 + a3b3
=
- a0b0 + a1b1
a2b2 + a3b3
= aμbμ
Therefore
a'μb'μ = aμbμ = invariant
Remark:
aμbμ = (a0, a)(b0, b) =
(a0, a)(- b0, b) = (- a0, a)(b0, b) =
= ( a0, a)(b0, b) = aμbμ
Therefore
aμbμ = aμbμ
|
|