Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
|
Mathématiques 45: Algèbre vectorielle:
Opérations sur les vecteurs
Produit scalaire de deux vecteurs
1. Définitions
Un vecteur peut être multiplié par un autre vecteur.
Ce produit s'appelle le produit scalaire de
ces deux vecteurs. On le note par un point •.
Le produit scalaire du vecteur par
le vecteur par
le vecteur s'ecrit: s'ecrit:
 • •
L'opération produit scalaire ou a multiplication
scalaire de vecteurs n'est pas la même que la multiplication
habituelle des nombres réels. Elle est différente. On la définit
de deux manières:
1.1. Méthode algébrique
1.1.1. La formule
On utilise la méthode algébrique lorsqu'on
connait les composantes des vecteurs.
Dans le plan cartésien, le produit scalaire de deux
vecteurs est égal à la somme des produits de leurs
composantes respectives.
Si  (a1, b1), (a1, b1), (a2, b2)
alors (a2, b2)
alors
 • • = a1a2 + b1b2 = a1a2 + b1b2
Le produit scalaire de deux vecteurs
est un scalaire .
1.1.2. Exemple
 (- 2, + 3), (- 2, + 3),  (+ 1, + 4) (+ 1, + 4)
 • • =
(- 2)(+ 1) + (+ 3)(+ 4) = - 2 + 12 = + 10. =
(- 2)(+ 1) + (+ 3)(+ 4) = - 2 + 12 = + 10.
1.2. Méthode géométrique
1.2.1. La formule
On utilise la méthode géométrique lorsqu'on
connait pas les composantes des vecteurs.
Dans le plan cartésien,
le produit scalaire de deux
vecteurs est égal au produit de leurs normes et du cosinus
de l'angle formé par ses deux vecteurs..
Si θ est l'angle formé par les vecteurs
 et et , ,
 • • =
|| =
|| |||| |||| || cos θ || cos θ
Le produit scalaire de deux vecteurs
est un scalaire .
1.2.2. Exemple
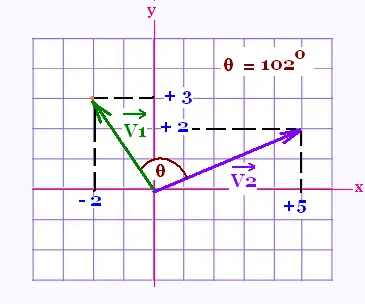
 (- 2, + 3), (- 2, + 3),
 (+ 5, + 2) (+ 5, + 2)
Algébriquement:
 • • = (- 2)(+ 5) + (+ 3)(+ 2) = - 10 + 6 = - 4. = (- 2)(+ 5) + (+ 3)(+ 2) = - 10 + 6 = - 4.
Géométriquement:
 • • =
|| =
|| |||| |||| || cos θ || cos θ
Les normes respectives des deux vecteurs sont:
|| || = √[(+ 5)2 + (+ 2)2] = √29, || = √[(+ 5)2 + (+ 2)2] = √29,
|| || = √[(- 2)2 + (+ 3)2] = √13. || = √[(- 2)2 + (+ 3)2] = √13.
θ = 102° ,
donc
cos θ = - 0.208
Ainsi:
 • • =
(√29) (√13) (- 0.208) = - 4 =
(√29) (√13) (- 0.208) = - 4
2. Projection d'un vecteur sur une droite
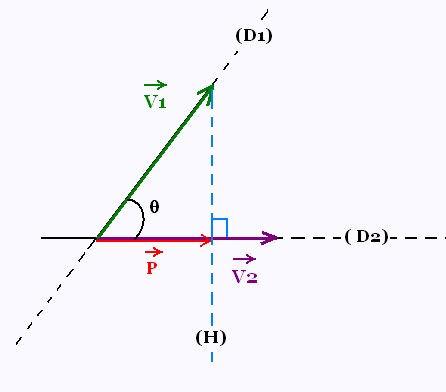 On considère deux vecteurs
On considère deux vecteurs  et et faisant un angle θ entre eux, de supports respectifs
(D1) et (D2). faisant un angle θ entre eux, de supports respectifs
(D1) et (D2).
À partir du sommet du vecteur  , on dresse
la perpendiculaire (H) au support de , on dresse
la perpendiculaire (H) au support de  . .
Cette perpendiculaire (H) coupe le support (D2) en l'extrémité
du vecteur 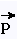 . .
Le vecteur 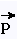 est la projection orthogonale
du vecteur est la projection orthogonale
du vecteur  sur la droite (D2), ou
la projection orthogonale de sur la droite (D2), ou
la projection orthogonale de sur sur .
.
Le vecteur 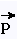 est colinéaire au
vecteur est colinéaire au
vecteur  . .
La définition du cosinus d'un angle permet d'ecrire:
cos θ = ||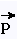 ||/|| ||/|| || ||
D'où
||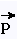 || = || || = || || cos θ || cos θ
En substituant cette relation dans la formule
du produit scalaire, on obtient:
 • • =
|| =
||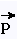 |||| |||| || ||
3. Vecteurs orthogonaux
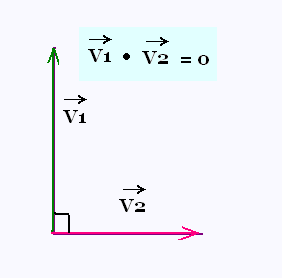 Un vecteur est orthogonal à un autre
s'ils forment un angle droit entre
eux.
Un vecteur est orthogonal à un autre
s'ils forment un angle droit entre
eux.
Si l'angle formé par deux vecturs est droit, alors
son cosinus est nul (cos 90° = 0) et donc
le produit scalaire des deux vecteurs est nul.
En effet, si l'angle θ formé par les vecteurs et
et est égal à 90° cela
implique cos θ = 0, et donc est égal à 90° cela
implique cos θ = 0, et donc
 • • =
|| =
|| |||| |||| || x 0 = 0; || x 0 = 0;
☛
 ⊥ ⊥
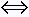
 • • = 0 = 0
4. Utilisation des vecteurs
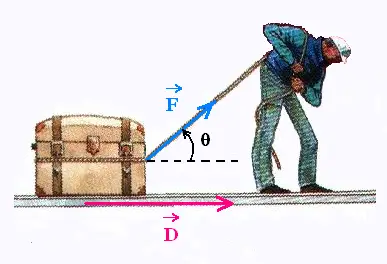
Les vecteurs sont très utile en Physique.
Ils représentent les forces, les vitesses, les déplacements,
les accélérations, les champs,...
Le produit scalaire est utilisé pour calculer le travail d'une force, le flux d'un champ, ...
On se souviendra que le travail d'une force 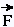 qui s'exerce sur un corps le faisant déplacer de
qui s'exerce sur un corps le faisant déplacer de 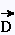 est égal au scalaire W =
est égal au scalaire W = 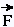 • • 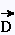 = || = ||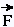 || || || ||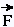 || cos θ . || cos θ .
||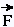 || en Newton (N),
|| || en Newton (N),
||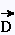 || en mètre (m), et
W en Joules (J). || en mètre (m), et
W en Joules (J).
|
|