Algèbre : fonction quadratique

1. Ce que l'on doit retenir :

La fonction quadratique f de la variable x s'ecrit sous

• forme générale : f(x) = a x² + b x + c
• forme quadratique : f(x) = a(x - h)² + k
• forme factorisée : f(x) = a (x - x₁) (x - x₂)

On peut passer d'une forme à une autre à l'aide de manipulation algébrique.
$$\large\bf\color {indigo}{ h = \frac {- b}{2a}} \;\;\;\;\;\;\;\; \large\bf\color {indigo}{ k = \frac {4 a c - b^2}{4a}}$$ h est l'abscisse du sommet et k son ordonnée.


Les solutions, si elles existent, de l'equation f(x) = 0 sont x₁ et x₂ appelées les zéros de la fonction. Elles sont calculés et présentés sous la formule quadratique suivante :

$$\large\bf\color {brown}{ x = \frac {- b \pm \sqrt{b^2 - 4 a c}}{2a}}$$

2. Exemples

Exemple 1

Pour chacune de ces fonctions quadratiques suivantes:

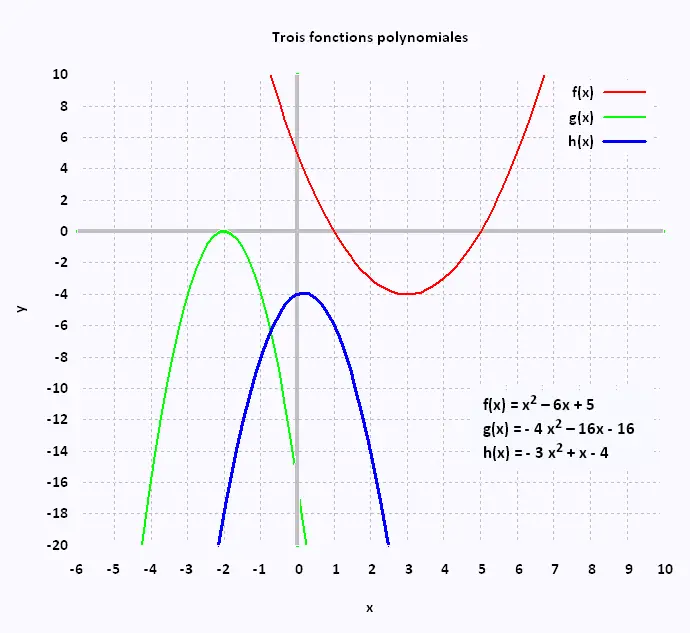
f(x) = x² – 6x + 5
g(x) = - 4 x² – 16x - 16
h(x) = - 3 x² + x - 4

déterminez les propriétés suivantes :

a) L’équation de l’axe de symétrie
b) l’image de la fonction
c) les coordonnées du sommet
d) l’ordonnée à l’origine
e) le maximum ou le minimum
f) les zéros
g) l’intervalle de croissance
h) l’intervalle de décroissance
i) les intervalles où la fonction est positive
j) les intervalles où la fonction est négative

f(x) = x² – 6x + 5
f(x) = (x² - 6x + 9) – 9 + 5
f(x) = (x – 3)² – 4
f(x) = (x – 3 - 2)(x - 3 + 2)
f(x) = (x – 5)(x - 1)
0 = (x – 5)(x - 1)

x = 5 ou x = 1 : Deux racines distinctes

a = 1, b = - 6, c = 5
h = 3, k = - 4

g(x) = - 4x² – 16x – 16
g(x) = - 4(x² + 4x + 4)
g(x) = - 4(x + 2)²
g(x) = - 4(x + 2)²
0 = - 4(x + 2)(x + 2)

x = - 2 ou x = - 2 : une racines double

a = - 4, b = - 16 , c = - 16
h = - 2, k = 0

h(x) = - 3 x² + x – 4
h(x) = - 3 [(x² – (1/3)x + 1/36) – 1/36 + 4/3]
h(x) = - 3 [(x² – 2(1/6)x + 1/36) – 1/36 + 4/3]
h(x) = - 3 [(x – 1/6)² + 47/36]
h(x) = - 3(x – 1/6)2 - 47/12

b² - 4 a c = (1)² - 4(- 3)(- 4) = (1)² - 4(- 3)(- 4) = 1 - 48 = - 47 est négatif, donc

L'équation n'a pas de racines.

a = - 3, b = 1 , c = - 4
h = 1/6, k = - 47/12

fonction	f(x)	g(x)	h(x)
(a)	x = 3	x = - 2	1/6
(b)	[4, +∞	]-∞,0]	]-∞ - 47/12]
(c)	(3,- 4)	(- 2, 0)	(1/6, - 47/12)
(d)	5	- 16	- 4
(e)	minimum - 4	maximum 0	maximum - 47/12
(f)	1 et 5	- 2	aucun
(g)	[3, +∞[	]- ∞, - 2]	]- ∞, 1/6]
(h)	]-∞,3]	[- 2, + ∞[	[1/6, + ∞[
(i)	]- ∞,1] ∪ [5, +∞[	- 2	aucun
(j)	[1,5]	R	R

Exemple 2

Il est possible de transformer la règle d’une fonction quadratique de la forme générale à la forme canonique en utilisant des manipulations algébriques. Observez l’exemple ci-contre:

x² + 8 x + 3
= x² + 8 x + 16 - 16 + 3
= (x² + 8 x + 16) - 13
= (x + 4)² - 13

a) En procédant de la même façon, transformez les règles suivantes sous la forme canonique

f₁(x) = x² – 4x + 1
f₂(x) = x² + 3x - 4
f₃(x) = x² - x - 1

b) Pour toutes les fonctions précédentes, le paramètre a est égal à 1. Comment pourrait-on procéder, à l’aide de manipulations algébriques comme celles-ci-dessus, pour obtenir la forme canonique si le paramètre a était différent de 1?

Appliquez votre méthode à la fonction
f₄(x) = 3x² – 6x + 5.

a) f₁(x) = x² – 4x + 1
= x² – 4x + 4 - 4 + 1
= (x² – 4x + 4) - 4 + 1
= (x - 2)² - 3

f₁(x) = (x - 2)² - 3

f₂(x) = x² + 3x - 4
= x² + 2(3/2) x + 9/4 - 9/4 - 4
= (x² + 2(3/2) x + 9/4) - 9/4 - 4
= (x + 3/2)² - 25/4

f₂(x) = (x + 3/2)² - 25/4

f₃(x) = x² - x - 1
= x² - 2(1/2) x + 1/4 - 1/4 - 1
= (x² - 2(1/2) x + 1/4) - 1/4 - 1
= (x - 1/2)² - 5/4

f₃(x) = (x - 1/2)² - 5/4

b) f₄(x) = 3x² – 6x + 5
= 3(x² - 2x) + 5
= 3(x² - 2x + 1 - 1) + 5
= 3(x² - 2x + 1) - 3 + 5
= 3 (x - 1 )² + 2

f₃(x) = 3(x - 1)² + 2