Mathématiques
2
Propriétés des
nombres entiers
Calculateurs
Exercices de
perfectionnement
© The scientific sentence. 2010
| |
|
Mathématiques 45: Arithmétique et Géométrie
Euclide et le traité Les Éléments
1. Les Éléments
Euclide est un mathématicien de la Grèce antique. Né vers 325 et
mort vers 265 av. J.C.
Euclide est l'auteur du traité de Mathématiques
Les Élements ecrit vers les années 300 av. J.C.
Les Éléments sont un traité d'Arithmétique et de Géométrie,
constitué de 13 livres:
• Le livre I énonce les propriétés de base de la géométrie:
Le théorème de Pythagore, somme des angles du triangle,
les trois cas d'isométrie des triangles.
• Le livre VI traite de l'application des proportions
à la géométrie : théorème de Thalès, figures semblables.
• Le livre VII traite des nombres:
divisibilité, nombres premiers, pgcd, et ppcm.
2. La division euclidienne
2.1. La méthode
En arithmétique, la division euclidienne ou division entière
est une opération de division qui fait intervenir quatre nombres entiers naturels:
Le dividende, le diviseur, le quotient et le reste.
Le quotient et le reste sont les résultats de l'opération de division
entière.
La division euclidienne se généralise aux entiers relatifs.
Ainsi à deux entiers naturels a et b, avec b non nul, la division
euclidienne produit deux uniques entiers naturels: un quotient
q et un reste r vérifiant l'égalité et l'inégalité suivantes:
a = bq + r et
r < b
2.2. Exemples
Exemple 1
On considère la division de 34 par 2:
34 = 2 x 10 + 14 n'est pas une division euclidienne parce que
le reste 14 n'est pas inférieur au diviseur 2 .
Exemple 2
On considère la division de 34 par 10:
34 = 10 x 2 + 14 n'est pas une division euclidienne parce que
le reste 14 n'est pas inférieur au diviseur 10 .
Exemple 3
On considère la division de 34 par 10:
34 = 10 x 3 + 4 est la division euclidienne parce que
le reste 4 est inférieur au diviseur 10 .
3. Algorithme d'Euclide
3.1. L'algorithme
L'algorithme d'Euclide est un algorithme qui permet
de déterminer le pgcd de deux nombres entiers. Cet algorithme
est traité dans le livre VII des Éléments.
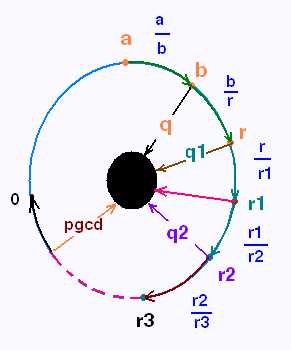
Nous allons démontrer la propriété suivante:
Le pgcd de deux nombres entiers est égal au
pgcd des derniers restes non nuls.
Soit a et b deux entiers naturels non nuls.
Soit r et q le reste et le quotient de la division euclidienne
de a par b:
a = b q + r
On a : b q = a - r
Soit d un divisuer de a et de b,
Si d est un diviseur de b, alors b/d est entier, donc (b/d)q = (a - r)/d
est aussi un entier. Ainsi d divise (a - r)
Puisque d divise a, c'est à dire a/d est entier et que (b/d)q
est entier, alors r/d doit être entier, donc d divise r.
Ainsi
Si d divise a et b , alors d divise r .
Autrement dit
Un diviseur de deux nombres est
aussi diviseur de leur reste.
On a : PGCD(a, b) = PGCD(b, r)
Et on continue ..
Si d divise b et divise r , alors d divise r et r1 :
b = r q1 + r1
On a : PGCD(b, r) = PGCD(r, r1)
Si d divise r et divise r1 , alors d divise r1 et r2:
r = r1 q1 + r2
On a : PGCD(r, r1) = PGCD(r1, r2)
....
Et ainsi de suite jusqu'à ce que le dernier
reste devient nul.
On a :
PGCD(a, b) = PGCD(b, r) = PGCD(r, r1) = PGCD(r1, r2) = .... =
PGCD(rn, ro).
L'avant dernier reste rn qui n'est pas nul est le pgcd
de a et b.
3.2. Exemple
On cherche le PGCD de 594 et 360.
L'algorithme d'Euclide donne:
594 = 360 x 1 + 234
360 = 234 x 1 + 126
234 = 126 x 1 + 108
126 = 108 x 1 + 18
108 = 18 x 6 + 0
Le dernier reste non nul est 18. Donc PGCD(594, 360) = 18.
PGCD(594, 360) = PGCD(360, 234) = PGCD(234, 126) = PGCD(126, 108)
= PGCD(108, 18) = PGCD(18, 0) = 18.
|
|
