Mathématiques 2: Rapport, taux et proportions
Pour comparer deux grandeurs ou deux quantités on utilise
le rapport ou le taux.
1. Le rapport
C'est la fraction ou la division de deux nombres qui correspondent
à deux grandeurs ou deux quantités de même nature exprimées
dans les mêmes unités.
Le rapport s’écrit sans unité sous l'une des trois formes suivantes:
a
- ou a:b ou a/b
b
Exemple:
Sebastien travaille quatre jours par semaine. Le rapport des
jours de travail de Sebastien à celui des jours de la semaine est
4
- ou 4:7.
7
Si deux rapports correspondent au même quotient, on dit qu'ils
sont équivalents
Par exemple
2 6
- et - sont 2 rapports équivalents.
5 15
2. Le taux
C'est la fraction ou la division de deux nombres qui correspondent
à deux grandeurs ou deux quantités de nature differente et
par conséquent exprimés à l'aide d'unités differentes.
Le taux s’écrit avec deux unités sous l'une des deux formes suivantes:
a
- ou a/b
b
Exemple 1
Sebastien lit des livres à raison de deux livres par trois mois.
Son taux de lecture est donc de
2
- ou 2/3.
3
On peut ecrire:
Il lit 2 livres en trois mois.
Il lit 2 livres par trois mois.
Il lit 2 livres chaque trois mois.
Il lit 2 livres en trois mois.
La comparaison est souvent exprimée à l’aide des mots
en, par, pour, chaque,
ou chacun.
Si deux taux correspondent au même quotient, on dit qu'ils
sont équivalents
2 livres/3 mois et 8 livres/an sont 2 taux équivalents
Exemple 2
Une voiture s'est déplacée de 180 km en deux heures.
Elle a donc roulé à raison de 180 km/2 h = 90 km/h
Le taux de déplacement ou la vitesse de la voiture
est de 90 km par heure ou en UNE heure.
Lorsqu'on réduit le dénominateur d'un taux à UN,
on dit que le taux est unitaire.
3. Les proportions
3.1. Définition
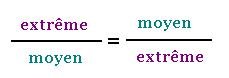Une proportionn est l'égalité de deux rapports
ou de deux taux. Elle est formée par quatres termes.
Le premier et le quatrième sont appelés les extrêmes ,
le deuxième et le troisième sont appelés les moyens .
3 6
- = - ou 3:7 = 6:14 est une proportion.
7 14
3 et 14 sont les extrêmes, 7 et 6 sont les moyens.
Propriété fondamentale de la proportion:
Dans une proportion, le produit des extrêmes est égal au produit des moyens
Pour l'exemple ci-dessus, nous avons:
3 x 14 = 7 x 6
3.2. Situation de proportionnalité
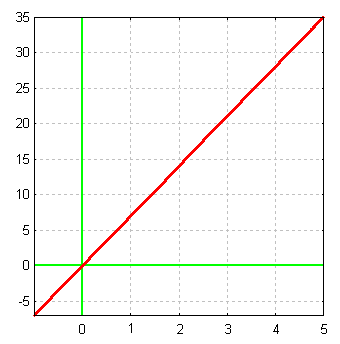
Une relation entre deux variables x et y où
tous les rapports ou les taux sont équivalents est
appelée situation de proportionnalité
Dans une telle situation, la représentation graphique est
une droite linéaire qui pass par l’origine.
Table des valeurs d'une situation de proportionnalité
Le rapport de proportionnalité est 2/14 = 3/21 = 5/35 = 1/7.
Puisque x/y = 1/7
Le coefficient de proportionnalité est
le nombre par lequel on multiplie le premier
terme pour obtenir le deuxième terme. Dans cet
exemple, il correspond à 7.
y = 7 x
3.2. Situation de proportionnalité inverse
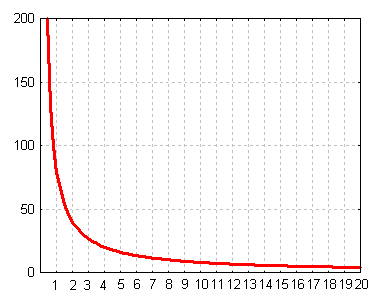
Une relation entre deux variables x et y dont
le produit des valeurs associées est constant est
appelée situation inversement proportionnalité ou
situation de variation inverse.
Dans une telle situation, le graphique est
une hyperbole.
Table des valeurs d'une situation inversement proportionnelle:
| x | 1 | 2 | 4 | 8 | 100 |
| y | 80 | 40 | 20 | 10 | 0.8 |
Le produit constant est x y = 80.
4. Résolution d'une situation de proportionnalité
Pour résoudre un problème d'une situation de proportionnalité,
on peut utilser trois méthodes:
4.1 Méthode du retour à l'unité
Cette méthode consiste à déterminer, à partir d'un rapport
ou d'un taux déjà connu, le rapport équivalent pour une unité,
et l'utiliser ensuite pour déduire les valeurs manquantes. b
Pour faire un pain, on utilise 500 g de farine et 10 g de sel.
Combien faut-il de sel pour 4 kg (4000 g) de farine?
Le rapport connu est 10:500 .
On effectue le retour à l'unité et on détermine le rapport
équivalent pour une unité de gramme farine:
10/500 = 0.02 g de sel pour une unité de masse
de farine.
Donc pour 4000 g de farine, il faut 4000 x 0.02 = 80 g de
sel.
4.1 Méthode du coefficient de proportionnalité
Cette méthode consiste à déterminer, à partir d'un rapport
ou d'un taux déjà connu, le coefficient de proportionnalité,
et l'utiliser ensuite pour déduire les valeurs manquantes.
Pour l'exemple du pain, le coefficient de proportionnalitéle
est le nombre qu'il faut multiplier par 500 pour trouver 10
qui est 0.02.
Donc pour 4000 g de farine, il faut 4000 x 0.02
= 80 de sel.
4.1 Méthode du facteur de changement
Cette méthode consiste à déterminer, à partir d'un rapport
ou d'un taux déjà connu, un rapport ou un taux équivalent,
en multipliant
et l'utiliser ensuite pour déduire les valeurs manquantes.
Pour l'exemple du pain, on
10/500 = 80 x 10 /80 x 500 = 80/4000
Donc 4000 g de farine corresponds à 80 de sel.
4.1 Propriété fondamentale de la proportion
Cette méthode du produit croisé consiste à utiliser la propriété
fondamentale de la proportion qui est:
Dans une proportion, le produit des extrêmes est égal au produit des moyens
Pour l'exemple du pain, on
10/500 = ?/4000
Donc ? = 0.02 x 4000 = 80 de sel.
5. Exercices
1. Les rapports et les taux
1. reduire les rapports:
2:12
30:33
46:120
23:69
49:7
18:12
2. Comparer les rapports dans chacun des cas,
en utilisant le symbole approprié > < ou =
11:2 ... 3:2
24:10 ... 4:5
8:20 ... 15:4
12:5 ... 2:3
55:10 ... 11:2
34:7 ... 17:2
3. Dans une première tasse de café de 100 mL, om met
5 g de sucre. Dans une deuxième de 80 mL, on met 10 g
de sucre. Quelle est la tasse la plus sucrée?
4. Deux voitures parcourent un distance de 120 km.
La première avec une vitesse de 80 km/heure, la
deuxième a mis 1 heure et demi pour parcourir cette
même distance. Laquelle des voitures est la plus rapide?
5.
Un technicien gagne 754 dollars par semaine. Quel est
son taux horaire s'il travaille 5 jours sur sept et
8 heures par jour ?
6. Determiner dans chaque cas la valeur qui permet
de former des rapports équivalents:
...:2 = 7:14
6:5 = ...:10
8:... = 1:4
12:6 = 2:...
...:24 = 12:16
7. Jimmy a mis 35 litres d'essence dans sa voiture
pour 45 $. Quel est le prix unitaire d'essence?
8.
La recette pour faire un pain est la suivante:
500 g de farine blanche
10 g de sel
10 g de levure
330 mL d'eau
Determiner la quantité d'ingrédients pour faire
4 pains.
9. On mélange 50 mL de colorant rouge avec
250 mL de peinture blanche. Pour avoir la même
teinte, combient faut-il de colorant avec 500 mL
de peinture blanche?
2. Situations de proportionnalité et
situations inversement proportionnelles
1.
Parmi les expressions suivantes, quelles sont qui
forment des proportions?
3:6 = 15:30
2:4 = 7:8
1:2 = 7:14
13 39
- = -
4 12
8 4
- = -
10 7
10 100
- = -
12 120
2. Dans chaque cas determine la valeur
qui permet de former une proportion:
2:3 = 12:...
...:5 = 100:20
14:17 = 42: ...
13 ...
- = -
4 12
8 4
- = -
... 7
... 100
- = -
12 120
3.
Voici un tableau de valeurs qui represente une consommation
en électricié pendant cinq mois. Le prix en dollars ($)varie
selon le kilo-Watt-heure (kWh) consommé. Representer
graphiquement cette situation et donner le rapport de
proportinnalité et le coefficient de proportinnalité.
| x ($) | 100 | 120 | 150 | 175 | 200 |
| y (kWh) | 2000 | 2400 | 3000 | 3500 | 4000 |
x
- est le rapport de proportinnalité.
y
y
- est le coefficient de proportinnalité.
x
4.
On veut distribuer 15 billets de 20 $ aux
élèves ayant un A+ en Mathématiques.
On prévoit le nombre de ces élèves entre 5 1t 15.
Compléter le tableau de valeurs ci-dessous et indiquer
de quel type de situation il s'agit.
x est le nombre d'élèves ayant un A+ en Mathématiques,
y est le l'argent en $ reçu par chacun des élèves.
| x | 5 | 6 | 10 | 12 | 15 |
| y | 60 | 50 | 30 | 25 | 20 |
5.
Daria a 150 $ en banque.
Elle veut économiser l'argent
pour acheter un Apple iPod
touch 32Go à 250$. Elle met
dans son compte en banque
20 $/semaine.
a) Compléter le tableau
suivant:
x est le nombre de semaine,
y est le montant d'argent
en $ déposé en banque.
| x | 0 | 1 | 2 | 5 | 10 | 15 |
| y | 0 | 20 | 40 | 100 | 200 | 300 |
b) représenter graphiquement cette
situation,
c) Au bout de combien de semaine, Daria aura-t-elle
la somme requise pour acheter son iPod?
6.
Le prix de location d'une voiture est de 300$ pour
une journée.
Solutions
|
