|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
| Electrostatics: Electric field
Some integrals
1. Integral: ∫dx/(x2 + R2)3/2
Let's find the following integral:
Let the following change of variable:
x/R = tg y
When x goes from - ∞ towards + ∞,
y goes from - π/2 towards + π/2.
Taking the derivative:
dx = R tg'y dy = R (1 + tg2y) dy
x2 + R2 = R2 tg2y + R2
= R2(1 + tg2y)
∫dx/(x2 + R2)3/2
= ∫ R (1 + tg2y) dy/(x2 + R2)3/2
= ∫ R (1 + tg2y) dy/ R3(1 + tg2y)3/2
= ∫ dy/ R2(1 + tg2y)1/2
= ∫ dy cos y/ R2
This integral is even, It follows that:
∫ dx/(x2 + R2)3/2
= 2 (1/ R2) ∫ dy cos y
= 2 (1/ R2) sin y (y: from 0 to + π/2)
= 2/R2
Now let's find the following integral:
Let the following change of variable:
z/y = tg θ
When z goes from - l towards + l,
θ goes from - arctan(l/y) towards + arctan(l/y).
from above, we have:
I = 2 (1/ y2) sin θ
from 0 towards + arctan(l/y)
We have
sin2θ = 1 - cos2θ =
1 - sin2θ/tan2θ, then
sin θ = tan θ/√(1 + tan2θ)
Hence
I = 2 (1/ y2) sin θ
θ : from 0 towards + arctan(l/y)
= 2 (1/ y2) [(sin(arctan(l/y) - sin(0)] =
2 (1/ y2) [(l/y)/√(1 + (l/y)2)] =
(2l/ y2)/√(y2 + l2)
2. Integral: ∫exp(ax) cosbx dx
We consider the following integral:
∫exp(ax) cosbx dx
I = ∫exp(ax) cos bx dx
By part;
exp(ax) = u and
dv = cos bx → v = (1/b)sin bx
I = exp(ax) (1/b)sin bx - ∫ (a/b)sin bx exp(ax) dx
= exp(ax) (1/b)sin bx - (a/b) ∫ sin bx exp(ax) dx
J = ∫ sin bx exp(ax) dx
u = exp(ax) dv = sin bx dx → v = - (1/b) cos bx
J = - (1/b) cos bx exp(ax) + (a/b)∫ exp(ax) cos bx
= - (1/b) cos bx exp(ax) + (a/b)I
I = exp(ax) (1/b)sin bx - (a/b)J
= exp(ax) (1/b)sin bx - (a/b)[- (1/b) cos bx exp(ax) + (a/b)I]
= exp(ax) (1/b)sin bx + (a/b)[ (1/b) cos bx exp(ax) - (a/b)I]
= exp(ax) (1/b)sin bx + (a/b2) cos bx exp(ax) - (a2/b2)I
(a2 + b2)/b2 I = exp(ax) (1/b)sin bx + (a/b2) cos bx exp(ax) (a2 + b2) I
= exp(ax) b sin bx + a cos bx exp(ax)
I = [b sin bx exp(ax) + a cos bx exp(ax)]/(a2 + b2)
∫exp(ax) cos bx dx =
exp(ax) [b sin bx + a cos bx]/(a2 + b2)
3. The probability Integrale
Using this integrale in Thermodynamics
J(n) = ∫ xn exp(- a x2)dx (1)
[- ∞ → + ∞]
The function to integrate : xn exp(- a x2) is odd and
therefore the integrale J(n) is null if n is odd.
It is even if n is even and therefore the integrale J(n) can be written as:
J(n) = 2. I(n) (2)
Where:
I(n) = ∫ xn exp(- a x2) dx [0 → + ∞]
I(n) = ∫ xn exp(- a x2)dx (3)
[0 → + ∞]
First, Let's integrate I(0).
I(0) = ∫ exp(- a x2) dx [0 → + ∞]
x is a dummy variable, thus:
I(0) = ∫ exp(- a y2) dy [0 → + ∞]
Multiplying the two equations, we get;
I2(0) = ∫ exp(- a x2) . ∫ exp(- a y2) dy [0 → + ∞]
= ∫ ∫ exp(- a x2 . exp(- a y2 dx dy [0 → + ∞] =
∫ ∫ exp[- a (x2 + y2)] dx dy [0 → + ∞] (4)
Let's switch to the polar coordinates:
r2 = x2 + y2
dxdy = r dr dθ
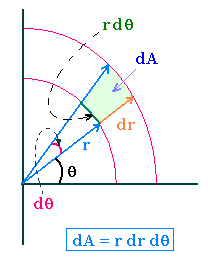
The equation (4) becomes:
I2(0) = ∫ exp[- a r2] r dr dθ [0 → + ∞ & 0 → π/2] (5)
(remark that the bouderies of the integrale are 0 and π/2 because r is limited to the first quadrant)
The equation (5) becomes:
I2(0) = (π/2) ∫ exp[- a r2] r dr [0 → + ∞] (6)
∫ exp[- a r2] r dr [0 → + ∞] is straightforward.
Let's substitute this way:
a r2 = z. Then dz = 2 a r dr. and r dr = dz/2a
Then: ∫ exp[- a r2] r dr = (1/2a)∫ exp[- z] dz =
- (1/2a)∫ exp[- z] [0 → + ∞] = 1/2a
The equation (6) becomes:
I2(0) = (π/2) (1/2a)= π/4a (7)
And:
I(0) = (π/2) (1/2a)= [π/4a]1/2 (8)
I(1) can be written as :
I(1) = ∫ x exp(- a x2 dx [0 → + ∞] (9)
From the relationships (6) and (7), it comes:
I(1) = (2/π)I2(0) = (2/π)I2(0) = (2/π)π/4a = 1/2a
I(1) = 1/2a
(10)
Now we will find I(2).
I(2) = ∫ x2 exp(- a x2 dx [0 → + ∞] (11)
Let's take the derivative of I(0):
dI(0)/da = d[∫ exp(- a x2 dx]/da [0 → + ∞] =
- ∫ x2 exp(- a x2 dx] [0 → + ∞] = - I(2) (12)
From the equation (8), we get:
dI(0)/da = d([π/4a]1/2)/da = (1/2)(π/4)1/2)(a)1/2 (-1/a2) =
- (π)1/2/4 a3/2 (13)
Equating (12) and (13), we get:
- I(2) = - (π)1/2/4 a3/2
Then:
I(2) = (π)1/2/4 a3/2
(14)
The derivative of I(1)is:
dI(1)/da = d[∫ x exp(- a x2 dx]/da [0 → + ∞] =
- ∫ x3 exp(- a x2 dx = - I(3)
From the equation (10), we get:
dI(1)/da = -1/2a2. Equating, we get:
- I(3) = -1/2a2. Then:
I(3) = 1/2a2
(15)
We can continue this way : taking the derivative
of
I(n) to get - I(n + 2) and
equating with dI(n)/da in
order to find I(n + 2).
Resuming, we have :
I(0) = [π/4a]1/2
I(1) = 1/2a
I(2) = (π)1/2/4 a3/2
I(3) = 1/2a2
...
By recurrence, the following is inferred:
For odd n:
I(n) = [(n - 1)/2]!/ 2 a(n + 1)/2
For even n:
I(n) = [π/a]1/2 [1.3.5. ... .(n - 1)]/2.(2a)n/2
|
|