|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
Summary: Gauss's law
1. Flux
The flux of the electric field E for a surface S is defined as
the surface integral of the electric filed over tis surface.
For a closed surface, the electric flux is:
The closed surface S for which the flux is evaluated
is an imaginary or mathematical surface called gaussian
surface.
2. Gauss's law
Gauss's law states that the flux for any closed surface
is equal to the net charge enclosed by that surface divided
by εo:
| |
|
|
→ → |
|
Σ q |
| ΦE = |
|
∯ |
E ⋅ dS |
= |
|
| |
|
|
|
|
εo |
Gauss's law follows from Coulomb's law and the
principle of superposition
3. Using Gauss's law to find the electric field
Gauss's law can be used to find the elcric field
produced by some highly symmetric charge distributions.
The important step is to select the gaussian surface.
Electric field for various charge distributions:
Charge distribution::
Near a long, straight, uniform line
charge, far from the end
Field magnititude;
E ≈ λ/2πεoR
Charge distribution::
Near a large, planar sheet of uniform surface charge,
far from the edges
Field magnititude;
E ≈ σ/2εo
Charge distribution::
Inside and outside a spherical shell of
uniform surface charge density
Field magnititude:
E = 0
(r < ro)
E = Q/4πεor2
(r > ro)
Charge distribution::
Inside and outside a sphere of uniform volume charge density
Field magnititude:
E = Qr/4πεoro3
(r < ro)
E = Q/4πεor2
(r > ro)
Charge distribution::
Inside a conductor
Field magnititude:
E = 0
Just outside a conductor
En = σ/εo,
and Et = 0
|
Electrostatics: Gauss's law
1. Flux
Flux, by definition is the rate at which a certain
quantity passes through an imaginary surface.
We are interested in the flux of an electric field or an
electric flux. We start by the electric flux of a uniform
field through a plane surface, and set Gauss's law that deals with
any curved surface or any nonuniform field, thereafter.
1.1. Flux of a uniform field through a plane
surface
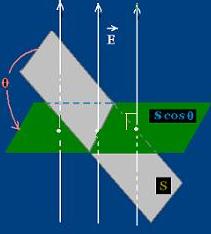
The flux ΦE of a vector field E is defined as
the dot product:
| |
|
→ → |
|
|
| ΦE = |
|
E ⋅ ΔS |
= |
E ΔS cos θ |
| |
|
|
|
|
S is the surface vector equal to the area S
of the surface times the unit normal vector n to that surface.
The angle θ is the angle between the two vectors
E and S.
The direction of the vector n is chosen such that it
points out of the enclosed surface.
The flux is a scalar quantity. The SI unit of electric flux
is N m2/C .
1.2. Flux of a field through a curved
surface
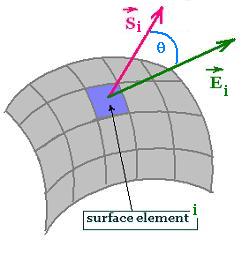
When the surface is curved or the electric field varies
from point to point over the surface, we divide this surface
in small surface elements; so each surface element is
then considered plane and the electric field through this small
surface is considered constant.
The flux trough the entire surface is the sum of the individual
contributions from each of the small surface elements:
Φ = Σ Φi = Σ Ei . ΔSi.
In the limit as the size of each surface element approaches
zero and their number approaches infinity, the sum becomes an
integral:
| |
|
|
→ → |
|
|
→ |
→ |
| ΦE = |
lim |
Σ |
Ei ⋅ ΔSi |
= |
∯ |
E |
dS |
| |
ΔSi→0 |
|
|
|
|
|
|
This is the expression of the flux of the electric field
E through S, called the surface integral of the vector
E over that surface.
When the surface of integration is closed, the symbol of
integration ∬ is replaced by
∯ .
The closed surface for which we calculate the flux is
an imaginary surface called gaussian surface, which
is not necessary the surface of the object.
The main task when we want to use Gauss's law is to
devise the appropriate gaussian surface.
2. Gauss's law
The electric flux for an arbitrary closed surface is
equal to the net charge enclosed by this surface
divided by εo.
In equation form:
| |
|
|
→ → |
|
Σ q |
| ΦE = |
|
∯ |
E ⋅ dS |
= |
|
| |
|
|
|
|
εo |
The closed surface, that is the gaussian surface for which
the flux is evaluated can of be any shape or size. Σq
is the net charge (positive charge minus negative charge) contained within the volume enclosed by the
surface.
3. Example
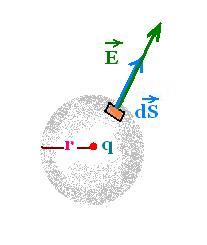
The simplest example of Gauss's law is the case of a point charge q
enclosed by a spherical gaussian surface of radius r, and placed at the center
of the sphere. The electric field from the point charge is radial and
fixed for a distance r, by symmetry, from the origin.
The electric field is perpendicular to all the surface elements over the
surface of the sphere.
Gauss's law gives:
∯ E . dS = Σq/εo =
E ∯ dS = q/εo
∯ dS = 4πr2
Therefore
E = (q/4πεo) . 1/r2 = k/r2
Point charge:
E = (q/4πεo) . 1/r2 = k/r2
This is the same result obtained with Coulomb's law.
4. Gauss's law from Coulomb's law
The electric field at the distance r from
the point charge q is given by the experimental
Coulomb's law:
We will use this expression to find Gauss's law.
4.1. Charged particle outside an arbitrary surface
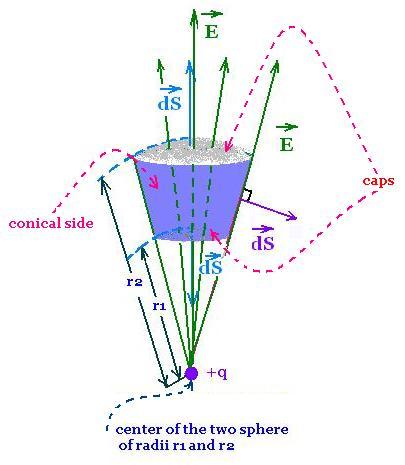
Any curved surface can be divided in infinitesimal
curved surfaces in the form of spherical caps.
The electric field through the curved surface
crosses this closed surface in two regions. The
first small is the region by which the field goes in
and the large second is the region by which the
field goes out.
We form an elementary closed surface
bounded by the two spherical caps and the
conical contour.
The electric field E(r) along the conical side is
perpendicular to its normal surface dS, so the
flux through the conical side is zero.
The flux through the first cap where the field
goes in is
Φin = - E(r1) dSin
The flux through the large cap where the field
goes out is
Φout = + E(r2) dSout
Therefore
The net flux through the closed surface bounded by the
two spherical caps and the conical side is:
Φnet = Φin + Φout
= - ∫ E(r1) dSin + ∫ E(r2) dSout
By symmetry, E(r) stay the same the long of the circumference
of radius r. So
∫ E(r1) dSin = E(r1) ∫ dSin
= 4π r12 E(r1)
And
∫ E(r2) dSout = E(r2) ∫ dSout
= 4π r22 E(r2)
And using Coulomb's law:
E(r1) = k q/r12
E(r2) = k q/r22
Therefore:
E(r2)/E(r1) = r12 /r22 =
Sin/Sout. So
E(r2) Sout = E(r1) Sin
That is:
Φout = - Φin
Hence
Φnet = Φin + Φout = 0
The flux is null through an arbitrary
surface which is
outside a charge.
4.2. Charged particle inside an arbitrary surface
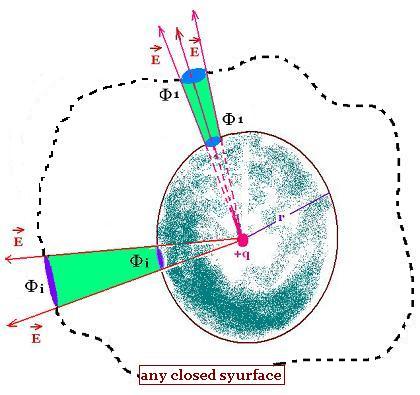
The electric field from the charge + q is radial.
Using the previous
result, the flux through an infinitesimal surface on the curved surface
is equal to the flux through the infinitesimal surface on the spherical
closed surface of radius r.
At r, The electric field is E(r) = k q/r2. so
Φ = ∫ E(r) dS = E(r) ∫ dS = k q/r2 x 4π r2 =
q/εo
The flux through an arbitrary surface
enclosing a charge q is euqal to q/εo .
4.3. Charged particles inside and outside
an arbitrary surface
In the case of many charged particles inside and
outside a gaussian surface, we use the principle of
superposition for the electric field. The
total electric field crossing a surface dS is the sum
of the individuals electric fields due to each charge.
The electric flux through a surface
dS is due to all the electric fields of different
charges. The net flux through any closed surface is
zero for ouside charges and Σqi/εo
for the conributions of the inside charges. Therfeore
The flux through an arbitrary shaped surface
enclosing charged particles qi
is equal to Σqi/εo
. Which is Gauss's law.
|
|