|
Electrostatics
Electromagnetics
Electricity &
Magnetism
© The scientific sentence. 2010
| Electrostatics: Applications of Gauss's law
We use Gauss's law to find the electric field due to a
charge distribution. The technique contains three steps:
1. Choose a gaussian surface (the crucial step),
2. Determine the flux through this curved surface,
3. Solve Gauss's law for E:
ΦE = ∫ E.dS =
Σqi/εo.
1. Field near a long line charge
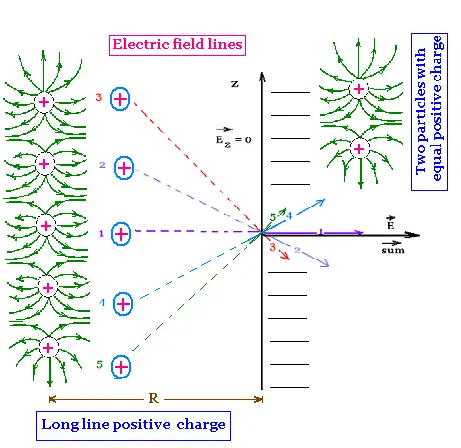
We want to determine an expression for the electric
field E at a point near the line charge and far
from its edges.
By symmetry, the electric field lines are straight
and parallel near the line and far from the end of
the wire. The lines are curves at the ends of the wire.
The wire is a long line charge straight and uniformly
charge with a linear charge density λ.
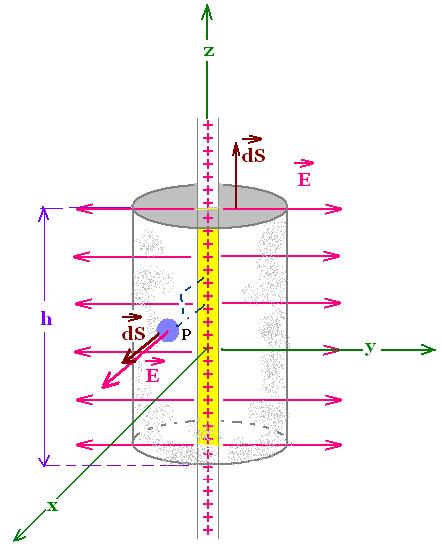
The first step, the most important, is to select
a gaussian surface. The symmetry of the distribution
of charge, then the symmetry of the field,
suggests a circular cylinder as a gaussian surface.
The wire is along the z-axis and the vector field is parallel
to the plane xoy. The chosen point is at the distance R
from the z-axis. λ is positive, so the
electric field points directly away from the z-axis.
Along the height of the cylinder h, E is perpendicular
to the lateral surface, so the related flux is:
ΦE(R) = ∫ E(R) dS = E(R)∫ dS =
2π R h E(R)
Through the top and the bottom of the cylinder,
the flux is zero because the vector electric field
is perpendicular to their normal surface dS.
The charge q inside the cylinder is q = λ h
Gauss's law gives therefore:
ΦE(R) = ∫ E(R) dS = 2π R h E(R) =
Σqi /εo = λ h /εo
Hence
2π R h E(R) = λ h /εo
Solving for E, we have
E(R) = λ /2πεo R
Infinitely long line charge:
E(R) = λ /2πεo R
2. Field near a large plane sheet of charge
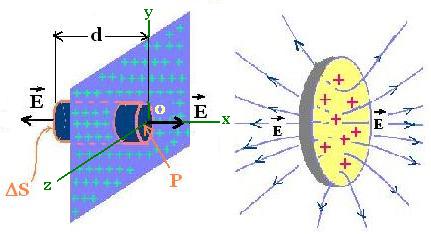
We want to determine an approximate expression of the electric
field at a point near a large plane sheet of charge (positive
with a uniform surface charge density σ), and
far from its edges.
First, to determine a gaussian surface, we examine the symmetry
of the situation:
Consider the plane sheet in the plane yoz. Since the origin
o in the plane yoz is far from the edges of the sheet, the field
E at a point P near the origin o will point directly out of the
plane yoz, perpendicular to this plane and parallel to the x-axis.
The field E from the point P points out of the sheet,
perpendicularly to this sheet toward the left side and toward
the right side.
Further, the electric field E far from the edges of the sheet and
near the origin o of the plane is uniform and depends on x only. We
assume that it is constant near the origin o, along a small distance
d.
A rotation of the point P about the x-axis does not change
the direction and the magnitude of the electric field E. So the
x-axis is the symmetry axis.
According to this symmetry of the field, we can select the gaussian
surface and set it as the right circular cylinder with axis along
the x-axis.
For this surface, the flux through the walls of the cylinder
is zero because the field is perpendicular to the normal surface
of the walls (lateral surface). The flux for each end of area
ΔS is
ΦE = ∫ E. dS = E ΔS + E ΔS = 2 E ΔS .
The charge enclosed by the gaussian cylinder is equal to
the product of the surface charge density σ and the
cross-sectional area, which is the same as the area of the
ends of the gaussian cylinder ΔS. Hence
Σqi = σΔS.
Gauss's law gives:
ΦE = Σqi or
2 E ΔS = σΔS/εo . Solving for E gives:
E = σ/2εo
This result is obtained from Coulomb's law.
Near a large plane sheet of
charge and far from its edges:
E = σ/2εo
3. Charged spherical shell
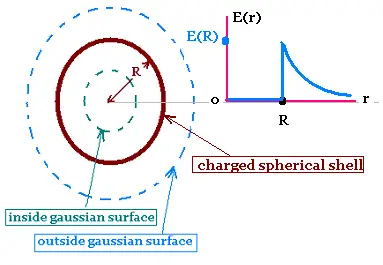
We want to determine the electric field inside
and outside a thin uniformly charged spherical shell
of radius R and charge q.
To select a gaussian surface, we determine the symmetry
of the field E first.
The charge distribution is spherical, then E is radial,
and its magnitude depends only on the distance r
from the center of the sphere. Therefore the gaussian
surface is the spherical surface that has the same
center as the spherical shell of charge, of radius
r < R inside and > R outside.
The flux inside is :
ΦE(r) = ∫ E(r). dS = E(r) ∫ dS =
4πr2 E(r)
The charge inside this surface is zero.
So
Σqi = 0.
Gauss's law gives:
ΦE(inside) = 0
That is
E(inside) = 0
The flux outside is :
ΦE(r) = ∫ E(r). dS = E(r) ∫ dS =
4πr2 E(r)
The charge inside this surface is q/εo.
Gauss's law gives:
ΦE(outside) = 4πr2 E(r) =
q/εo
Solving for E(r)
E(outside) = q/4πεo (1/r2)
Charged spherical shell:
E(inside) = 0
E(outside) = q/4πεo (1/r2)
4. Uniformly charged sphere
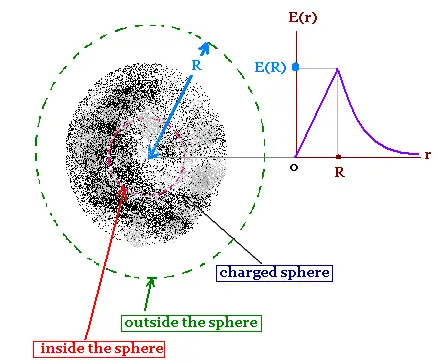
We want to determine the electric field inside and outside
a uniform spherical distribution of charge of radius R,
charge Q, and volume charge density ρ.
The electric field has only a radial component and depends only
on the distance from the center. Thus the gaussian surface is
the spherical surface with the same center as the charge
distribution.
Inside the sphere: r < R
The expression of the flux is:
ΦE(r) = ∫ E(r). dS = E(r) ∫ dS =
4πr2 E(r)
We have
q(r) = V ρ = (4/3)π ρ r3
q(R) = Q = V ρ = (4/3)π ρ R3
V is the volume of the charged sphere
Then
q(r) = Q r3/R3
ΦE(r) = Σqi/εo =
q/εo = Q r3/R3εo
Gauss's law gives:
4πr2 E(r) = Q r3/R3εo
Solving for E(r)
E(r) = Q r /4π εo R3
= ρ r /3εo
Outside the sphere: r > R
Gauss's law gives:
4πr2 E(r) = Q/εo
Solving for E(r)
E(r) = Q/4πεo (1/r2)
= ρR3/3εo (1/r2)
Uniformly charged sphere :
E(inside) = Qr/4πεoR3
= (ρ/3εo)r
E(outside) = Q/4πεo(1/r2)
= ρR3/3εo(1/r2)
We remark that a point charge Q, or the shell of charge Q
or a sphere of charge Q provides the same expression
for the electric field a distance r from them: E(r)
= Q/4πεo (1/r2).
|
|