Calculus III:

functions of more than one variable
Tangent planes
Linear approximation of a surface near a point

1. Equation of the tangent plane to
a surface at a point

The two partial derivatives f_x and f_y are the slopes of their corresponding traces.

The graph of a function z = f(x,y) is a surface in three dimensional space . We can then determine the equation of the plane that is tangent to the surface as a certain point.

Let’s consider a point (xo, yo) on the trace Cx to f(x,y) for the plane y = yo where x varies and y held fixed; and Cy the trace to f(x,y) for the plane x = xo where y varies and x held fixed.

The two partial derivatives f_x(xo, yo) and f_y(xo, yo) are the slopes of the tangent lines Lx and Ly to the traces Cx and Cy respectively. .

The point (xo, yo) is then located on both the surface and the plane. This point on the space has the coordinates (xo, yo, zo) = (xo, yo, f(xo,yo))

If (a,b,c) is a normal vector to the surface at the point (xo, yo, zo) , the the eqaution of the tangent plane is :

(x - xo)a + (y - yo)b + (z - zo)c = 0

Now, over Cx, where y = yo, the equation of the line Lx is

(x - xo)a + (z - zo)c = 0 or

z - zo = - (a/c)(x - xo)

The factor - (a/c) is the slope of the tangent line Lx to Cx and to the surface at the point (xo,yo,zo). It is then equal to f_x(xo,yo). Therefore

f_x(xo,yo) = - (a/c)

Similarly, hold x fixed at x = xo the equation of the tangent line Ly to Cy on the surface is

z - zo = - (b/c)(x - xo)

and

f_y(xo,yo) = - (b/c)

The equation of the tangent plane to the surface given by z = f(x,y) at the point (xo,yo) is then:

z - zo = (x - xo)f_x(xo,yo) + (y - yo)f_y(xo,yo)

With zo = f(xo,yo), the equation becomes:

z = f(xo,yo) + (x - xo)f_x(xo,yo) + (y - yo)f_y(xo,yo)

Example 1

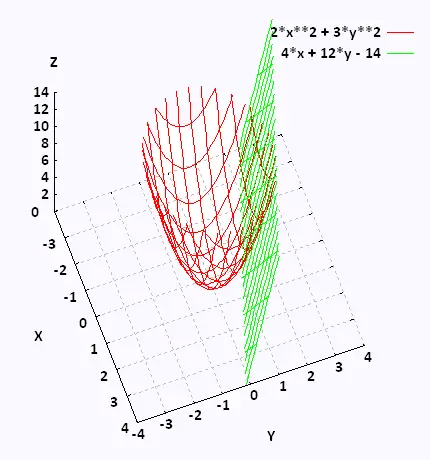
Find the equation of the tangent plane to
z = 2 x² + 3 y², at the point (1,2) .

f(x,y) = 2 x² + 3 y²
f_x = 4x
f_y = 6y
zo = f(1,2) = 14
f_x(1,2) = 4
f_y(1,2) = 12

The equation of the plane is then:

z = 14 + 4(x - 1) + 12(y - 2) =
14 + 4x - 4 + 12 y -24 = 4x + 12 y - 14

z = 4x + 12 y - 14

2. Linear approximation of a surface near a point

Near the point (xo,yo), the equation of the tangent plane remains T(x,y) ≅ f(xo,yo) + (x - xo)f_x(xo,yo) + (y - yo)f_y(xo,yo) that represents an approximation of the surface area near that point.

So as long as we are near to the point (xo, yo), the tangent plane could approximate the function at that point. This is a linear approximation:

Near the point (xo,yo),
f(x,y) ≅f(xo,yo) + (x - xo)f_x(xo,yo) + (y - yo)f_y(xo,yo)

Example 2

Find the linear approximation to z = 2 x² + 3 y², at the point (1,2) .

f(x,y) = 2 x² + 3 y²
f_x = 4x
f_y = 6y
zo = f(1,2) = 14
f_x(1,2) = 4
f_y(1,2) = 12

The equation of the plane is then:

z = 14 + 4(x - 1) + 12(y - 2) =
14 + 4x - 4 + 12 y -24 = 4x + 12 y - 14

The linear approximation is:

f(x,y) ≅ T(x,y) = 4x + 12 y - 14