Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Surfaces integrals of vector fields
We will work the oriented surfaces and their associated unit normal vectors , then evaluating surface integrals of vector fields.
1. Definitions
We evaluated line integrals of vector fields. Now
we are going to evaluate surface integrals of vector fields.
In line integrals calculus, the integration along a curve
is associated with the orientation of this curve.
In surface integrals, the normal vector to the surface
that is associated with. We talk then about oriented surface .
Let�s consider a surface that has two sides (Moebius strip has one side).
This means that the surface has a tangent plane at every point, so
every point has two unit normal vectors that have opposite directions.
Therefore, every surface have two sets of normal vectors. One set with an orientation, the second with the opposite direction. The chosen direction
will give an orientation to the surface.
We consider the particular case of a closed surface. A surface S is closed if it is the boundary of some solid region E. A good example of a closed surface is the surface of a sphere.
For the closed surfaces, the orientation is defined. By convention,
the closed surface S has a positive orientation if we choose the set of unit normal vectors that point outward from the inner region E while the negative orientation will be the set of unit normal vectors that point in towards the region E.
2. The normal vector to the surface
We want to determine the unit normal vector  to the surface, corresponding to the chosen orientation. We have two methods to do that: to the surface, corresponding to the chosen orientation. We have two methods to do that:
1. Using the gradient of the function ∇f
Let�s consider first, that the function of the surface S, over
we want to integrate, is given by z = g(x,y). In this case we can
define a new function: f(x,y,z) = z - g(x,y). So the surface
is defined by the function f of equation f(x,y,z) = 0.
We know that the gradient ∇f of a function f of equation f(x,y,z) = constant, is normal to the surface. So, the unit normal vector is then:
 = ∇f/|∇f| = ∇f/|∇f|
For this function,
∇f = 〈 - gx, - gy, 1 〉 . Hence:
 = 〈 - gx, - gy, 1 〉/|∇f|
=
- gx = 〈 - gx, - gy, 1 〉/|∇f|
=
- gx - gy
- gy + +  /|∇f| /|∇f|
The normal vector is then:
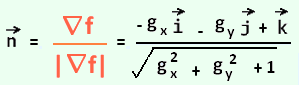
This unit vector gives a positive component of  ,
in the z-direction. So this normal vector will point upwards
de surface. With a closed surface, the component of ,
in the z-direction. So this normal vector will point upwards
de surface. With a closed surface, the component of  determine if the direction of the orientation. determine if the direction of the orientation.
Of course, a similar work done for z = g(x,y) can be done for the thoe other
forms of function y = g(x,z) or x = g(y,z).
2. Using the cross product  x x 
Here, we want to find the unit normal vector  , when the surface is given parametrically as: , when the surface is given parametrically as:
 (u,v) = x(u,v) (u,v) = x(u,v)  + y(u,v) + y(u,v)  + z(u,v) + z(u,v)  . .
We know that the vector cross product  x x 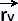 is normal to the tangent plane at a particular point on
the surface S over we integrate, hence normal to this surface at that point. is normal to the tangent plane at a particular point on
the surface S over we integrate, hence normal to this surface at that point.
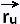 = ∂ = ∂ /∂u, and /∂u, and
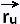 = ∂ = ∂ /∂v . /∂v .
So, in the case of parametric surfaces one of the unit normal vectors is:
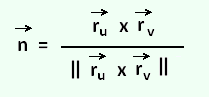
3. Surface integrals of vector fields
Now, we will evaluate surface integrals of vector fields.
Given a vector field  with unit normal vector with unit normal vector  , then the surface integral of the vector , then the surface integral of the vector  over the surface S is given by: over the surface S is given by:
∫∫S  . .  =
∫∫S =
∫∫S  . .  dS dS
This is called the flux of  across S. across S.
Let�s first start by assuming that the surface is given by z = g(x, y) with an upwards orientation; and the vector field is given by  = P = P + Q + Q + R + R . .
So the surface integral of  over S is: over S is:
∫∫S  . .  =
∫∫S =
∫∫S  . .  dS = dS =
∫∫D (P + Q + Q + R + R ) .
{(- gx ) .
{(- gx - gy - gy + +  )/√[(gx)2 +
(gy)2 + 1]} √[(gx)2 +
(gy)2 + 1] dA
= )/√[(gx)2 +
(gy)2 + 1]} √[(gx)2 +
(gy)2 + 1] dA
=
∫∫D (P + Q + Q + R + R ) .
(- gx ) .
(- gx - gy - gy + +  ) dA = ) dA =
∫∫D
(- P gx - Q gy + R) dA.
∫∫S  . .  =
∫∫D (- P gx - Q gy + R) dA =
∫∫D (- P gx - Q gy + R) dA
In the case we want to change the orientation, that is to be downward;
all what to do is to change the sign on the normal vector, so change the
sign on the integrand.
Of course, the derivation of each formula for y = g(x,z) or x = g(y,z)
is similar to that we just did for z = g(x,y).
• When the surface is given parametrically by  (u,v),
the formula for the surface integral is written: (u,v),
the formula for the surface integral is written:
∫∫S  . .  =
∫∫S =
∫∫S  . .  dS = dS =
∫∫D  .
{ .
{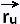 × × 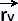 /| /|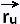 × × 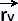 |}
| |}
|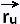 × × 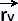 |
dA
= |
dA
=
∫∫D  .
( .
(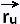 × × 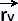 ) dA ) dA
∫∫S  . .  =
∫∫D =
∫∫D  . ( . (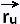 × × 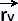 ) dA ) dA
Example 1
Evaluate ∫∫S
 . . 
Where  = y = y + z + z . .
S is the surface given by the paraboloid:
y = x2 + z2
,
0 ≤ y ≤ 1, and the disk x2 + z2 ≤ 1 at y = 2 .
Consider that S has positive orientation, so the normal vector are oriented
upwards.
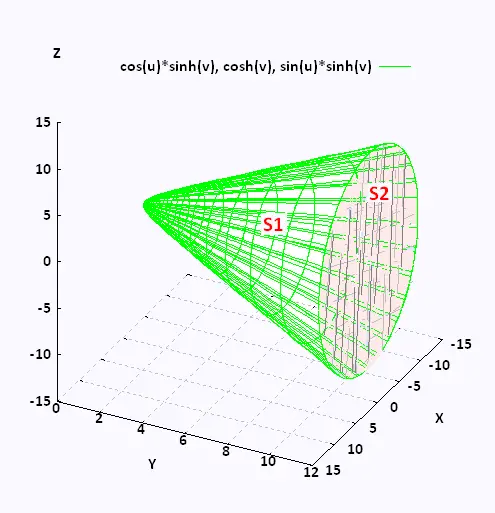 The paraboloid part (S1) and the disk (S2) form a closed surface S = S1∪S2. The surface has a positive orientation. So, all the unit normal vectors point outwards from the region enclosed by S. For the paraboloid they point in the negative y direction, for the disk they point in the positive y direction.
The paraboloid part (S1) and the disk (S2) form a closed surface S = S1∪S2. The surface has a positive orientation. So, all the unit normal vectors point outwards from the region enclosed by S. For the paraboloid they point in the negative y direction, for the disk they point in the positive y direction.
To get the overall surface integral, we do the surface integral on each and then add the results.
1. For the paraboloid (S1):
We have the surface in the form y = g(x,z) or
f(x,y,z) = y - x2 - z2 = 0. So
fx = - 2 x,
fy = 1 , and
fx = - 2 z.
The gradient vector of this function is then:
∇f = 〈 - 2 x , 1, - 2z 〉
The y component (+ 1) of the gradient is positive. So this vector will point in the positive y direction. But we need the normal vector to point in the negative y direction so that it will be pointing away from the enclosed region. We set then the n�gative sign with the normal vector.
∇f = - 〈 - 2 x , 1, - 2z 〉.
Therefore
∫∫S1  . .  =
∫∫D - 〈 0 , y, z 〉 . 〈 - 2 x , 1, - 2z 〉 dA = =
∫∫D - 〈 0 , y, z 〉 . 〈 - 2 x , 1, - 2z 〉 dA =
∫∫D - (y - 2z2) dA =
∫∫D - (x2 + z2 - 2z2) dA =
∫∫D - (x2 - z2) dA.
∫∫S1  . .  =
∫∫D - (x2 - z2) dA. =
∫∫D - (x2 - z2) dA.
D is the disk of radius 1 in the xz-plane. So it is convenient to use polar coordinates to complete this integral.
The polar coordinates for this region are:
x = r cos θ , z = r sin θ with
0 ≤ r ≤ 1 and 0 ≤ θ ≤ 2π
∫∫D - (x2 - z2) dA =
∫02π
∫01 - (r2cos2 θ - r2sin2 θ) r dr dθ =
∫02π
∫01 - (cos2 θ - sin2 θ) r3 dr dθ =
(1/4)∫02π
∫01 - (cos2 θ - sin2 θ) dθ =
(1/4)∫02π
∫01 - (cos 2θ) dθ =
(1/8)
∫01 - (sin 2θ)|02π = 0
Therefore
∫∫S1  . .  =
0 =
0
2. For the disk (S2):
We have the surface in the form y = 2 or
f(x,y,z) = y - 2 = 0. So
fx = 0,
fy = 1 , and
fz = 0.
The gradient vector of this function is then:
∇f = 〈 0 , 1, 0 〉 =  . .
The y component (+ 1) of the gradient is positive. So this vector will point in the positive y direction. Indeed we need the normal vector to point in the positive y direction so that it will be pointing away from the enclosed region. We set then the positive sign with the normal vector.
∇f = + 〈 0, 1, 0 〉.
Therefore
∫∫S2  . .  =
∫∫D 〈 0 , y, z 〉 . 〈 0 , 1, 0 〉 dA =
∫∫D y dA = =
∫∫D 〈 0 , y, z 〉 . 〈 0 , 1, 0 〉 dA =
∫∫D y dA =
∫∫D (2) dA = 2 ∫∫D dA.
∫∫S2  . .  =
2∫∫D dA. =
2∫∫D dA.
D is the disk of radius 1 in the xz-plane. So dA = dx dz.
2 ∫∫D dA = 2 π 12 = 2 π.
Therefore
∫∫S2  . .  =
2π =
2π
Adding the two parts up, the surface integral is:
∫∫S  . .  =
∫∫S1 =
∫∫S1  . .  +
∫∫S2 +
∫∫S2  . .  =
0 + 2π = 2π. =
0 + 2π = 2π.
∫∫S  . .  =
2π. =
2π.
Example 2
Evaluate ∫∫S
 . .  ,
where ,
where  = x = x + y + y + z + z . .
S is the upper half of the sphere :
x2 + y2 + z2 = 4
,
and the disk x2 + y2 ≤ 4 in the plane z = 0.
Consider that S has positive orientation, so the normal vector are oriented
upwards.
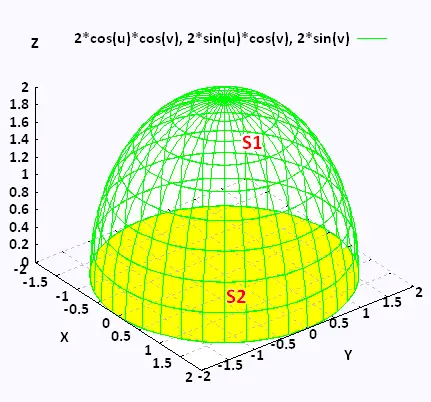 The half of the sphere part (S1) and the disk (S2) form a closed surface S = S1∪S2. The surface has a positive orientation. So, all the unit normal vectors point outwards from the region enclosed by S. For the sphere they point in the positive z direction, for the disk they point in the negative z direction.
The half of the sphere part (S1) and the disk (S2) form a closed surface S = S1∪S2. The surface has a positive orientation. So, all the unit normal vectors point outwards from the region enclosed by S. For the sphere they point in the positive z direction, for the disk they point in the negative z direction.
To get the overall surface integral, we do the surface integral on each and then add the results.
1. For the hemisphere (S1):
Since the surface is a hemisphere, we will need to use
the parametric representation of the surface:
 (θ φ) = 2 sin θ cos φ (θ φ) = 2 sin θ cos φ
 + 2 sin θ sin φ
+ 2 sin θ sin φ 2 cos θ
2 cos θ
With 0 ≤ θ π/2 and 0 ≤ φ 2π .
 (θ φ) = ∂r/∂θ = (θ φ) = ∂r/∂θ =
2 cosθ sin φ +
2 cos θ sin φ +
2 cos θ sin φ - 2 sin θ
- 2 sin θ
 (θ φ) = ∂r/∂φ = (θ φ) = ∂r/∂φ =
- 2 sin θ sin φ +
2 sin θ cos φ +
2 sin θ cos φ
 × ×  = =
- 4 sin2 θ cos φ - 4 sin2 θ sin φ
- 4 sin2 θ sin φ - 4 sin θ cos θ
- 4 sin θ cos θ
 = ( = ( × ×  )/| )/| × ×  | |
The z component (- 4 sin θ cos θ) of the gradient is negative. So this vector will point in the negative y direction. But we need the normal vector to point in the positive z direction so that it will be pointing away from the enclosed region. We set then the n�gative sign with the normal vector. So
 = - ( = - ( × ×  )/| )/| × ×  |
= |
=
(
4 sin2 θ cos φ +
4 sin2 θ sin φ +
4 sin2 θ sin φ +
4 sin θ cos θ +
4 sin θ cos θ )
| )
| × ×  | |
 ( ( (θ, φ) =
2 sin θ cos φ (θ, φ) =
2 sin θ cos φ  +
2 sin θ sin φ +
2 sin θ sin φ  +
2 cos θ +
2 cos θ 
 ( ( (θ, φ) .
( (θ, φ) .
( × ×  ) = ) =
8 sin3 θ cos2 φ +
8 sin3 θ sin2 φ +
8 sin θ cos2 θ =
8 sin3 θ +
8 sin θ cos2 θ.
 ( ( (θ, φ) .
( (θ, φ) .
( × ×  ) =
8 sin3 θ +
8 sin θ cos2 θ ) =
8 sin3 θ +
8 sin θ cos2 θ
8 ∫∫S2  . .  =
∫∫D (sin3 θ +
sin θ cos2 θ) dA
= =
∫∫D (sin3 θ +
sin θ cos2 θ) dA
=
8 ∫∫D (sin3 θ +
sin θ cos2 θ ) dθ dφ =
8 ∫02π
∫0π/2
sin θ (1 - cos2 θ +
sin θ cos2 θ ) dθ
dφ =
8 ∫02π
∫0π/2
sin θ dθ
dφ =
8 ∫02π
(1)
dφ = 8 x 2 π = 16 π
∫∫S1  . .  =
16 π =
16 π
2. For the disk (S2):
We have the surface in the form z = 0 or
f(x,y,z) = z = 0. So
fx = 0,
fy = 0 , and
fz = 1.
The gradient vector of this function is then:
∇f = 〈 0 , 0, 1 〉 =  . .
The z component (+ 1) of the gradient is positive. So this vector will point in the positive z direction. But we need the normal vector to point in the negative z direction so that it will be pointing away from the enclosed region. We set then the negative sign with the normal vector.
∇f = - 〈 0, 0, 1 〉 = -  .
Therefore .
Therefore
∫∫S2  . .  =
- ∫∫D 〈 x , y, z 〉 . 〈 0 , 0, 1 〉 dA = =
- ∫∫D 〈 x , y, z 〉 . 〈 0 , 0, 1 〉 dA =
- ∫∫D z dA =
∫∫D (0) dA = 0.
Therefore
∫∫S2  . .  =
0 =
0
Adding the two parts up, the surface integral is:
∫∫S  . .  =
∫∫S1 =
∫∫S1  . .  +
∫∫S2 +
∫∫S2  . .  =
16π + 0 = 16π. =
16π + 0 = 16π.
∫∫S  . .  =
16π. =
16π.
|
|