Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Surface area
Surface area of a solid of revolution
We are going to determine the surface area of a solid of revolution.
The surface area of a solid obtained by rotating a function about the
x or y axis is already determined in Calculus II. But here it is about
a function of two dimentions.
1. Surface area element
Now, we want to find the area of the surface given by z = f(x,y)
(x,y) is a point from the region D in the xy-plane over we
integrate the fuction z.
The differential surface element, in three-dimentional
space, is:
dS = √[∂f/∂x)2 +
(∂f/∂y)2 +
1]dA.
dA = dx dy , the differential surface area element.
∂f/∂x = fx, and ∂f/∂y = fz
. Therefore
dS = √[(fx)2 +
(fy)2 + 1]dA
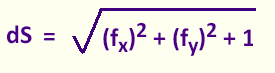
Example 1
Find the triangle surface S area of the part of the plane
x + y + z = 1, formed by the vertices (0,1,0),
(1,0,0), and (0,0,1) that lies in the first octant.
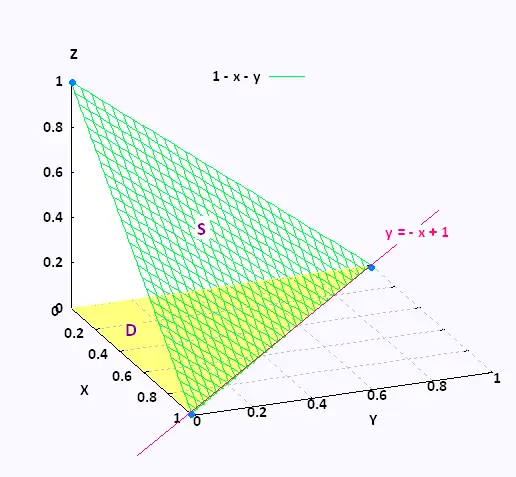
The surface S correspond to the area D on the xy-plane.
We denote by dA the area element in the the domaine D
where we integrate. Here dA = dx dy .
The function in the form z = f(x,y) is, by solving for z
the equation of the triangle plane x + y + z = 1:
z = 1 - x - y
Taking the partial derivatives gives:
fx = - 1, and
fy = - 1
. Therefore
dS = √[(fx)2 +
(fy)2 + 1] dA = √[(-1)2 +
(-1)2 + 1] dA = √3 dA.
dS = √ 3 dA
The limits defining D are:
0 ≤ x ≤ 1
0 ≤ y ≤ 1 - x
Now Let's evaluate S
S = ∫∫S f(x,y) dS = ∫∫D f(x,y) dA =
∫01
∫01-x
(1 - x - y) dy dx =
∫01
(y - xy - (1/2)y2)|01-x dx =
∫01
(1/2)(1 - x)2 dx =
(1/6)(x - 1)3|01 = 1/6
Therefore
S = ∫∫S (1 - x - y) dS =
= 1/6
Exercice
Evaluate ∫∫S × ×  , where , where
 =
= xy =
= xy  yz
yz  +
zx +
zx  , and , and
S is the upper half of the sphere
x2 + y2 + z2 = 4, of base the disk
x2 + y2 = 4 in the plane z = 0.
Consider that S has the positive orientation.
Evaluate result1 and result2 written below:

The surface is composed by S1 (hemi-sphere) and S2 (disk):
S = S1∪S2,
1) The hemi-sphere (S1):
S1 is a sphere, we need then to use the parametric
representation of the surface according to spherical coordinates:
 (θ, φ) =
2 sin θ cos φ (θ, φ) =
2 sin θ cos φ  +
2 sin θ sin φ +
2 sin θ sin φ  +
2 cos θ +
2 cos θ  , with the limits: , with the limits:
0 ≤ θ ≤ π/2 0 ≤ φ ≤ 2π
Now we determine:
 =
∂ =
∂ (θ, φ)/∂θ, and (θ, φ)/∂θ, and
 =
∂ =
∂ (θ, φ)/∂φ (θ, φ)/∂φ
and, we determine their cross product:
 × ×  = =
- 4 sin2 θ cos φ  - 4 sin2 θ sin φ
- 4 sin2 θ sin φ  - 4 sin θ cos θ
- 4 sin θ cos θ 
The component of  is negative, so is negative, so
 = - = -  × ×  /| /| × ×  | = | =
4 sin2 θ cos φ  +
4 sin2 θ sin φ +
4 sin2 θ sin φ  +
4 sin θ cos θ +
4 sin θ cos θ  /
| /
| × ×  | |
Next
 ( ( (θ, φ)) = (θ, φ)) =
4 sin θ cos φ sin θ sin φ  4 sin θ sin φ cos θ
4 sin θ sin φ cos θ  +
4 sin θ cos φ cos θ +
4 sin θ cos φ cos θ  . .
We need also to calculate the scalar product :
 ( ( (θ, φ)) .
( (θ, φ)) .
( × ×  ) =
result 1 ) =
result 1
Therefore
∫∫S1  . .  =
∫∫S1 =
∫∫S1 . .  dS dS
Since dS = | × ×  | dA, | dA,
∫∫S1  . .  = =
= ∫∫D  .
( .
( × ×  /| /| × ×  |) | |) | × ×  | dA = | dA =
= ∫∫D  .
( .
( × ×  ) dA =
∫02π
∫0π/2 ) dA =
∫02π
∫0π/2  .
( .
( × ×  ) dθ dφ = ) dθ dφ =
∫02π
∫0π/2
result 1
dθ dφ = result 2
2) The disk (S2)
For the disk at the bottom  must be equal to
- must be equal to
-  . .
∫∫S2  . .  =
∫∫S2 =
∫∫S2 . (- . (-  ) dS
=
∫∫S2 ) dS
=
∫∫S2 . (- . (-  ) dS ) dS
We have:
 . (- . (-  ) =
〈xy, yz, zx 〉 . 〈0, 0, -1 〉
= - xz.
Then ) =
〈xy, yz, zx 〉 . 〈0, 0, -1 〉
= - xz.
Then
∫∫S2 . (- . (-  ) dS =
- z ∫∫D x dA at z = 0 . So
∫∫S2 ) dS =
- z ∫∫D x dA at z = 0 . So
∫∫S2  . .  = 0 = 0
Therefore
∫∫S  . .  =
∫∫S1 =
∫∫S1  . .  +
∫∫S2 +
∫∫S2  . .  = =
result 2 + 0 = result 2.
|
|