Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Stokes' theorem
Green�s Theorem links the line integral to a double integral over the region
delimited by an oriented curve.
In this section we are going to to work on Stokes' theorem that likes
a line integral to a surface integral.
Stokes' theorem is a higher dimensional version of Green�s Theorem.
1. Definitions
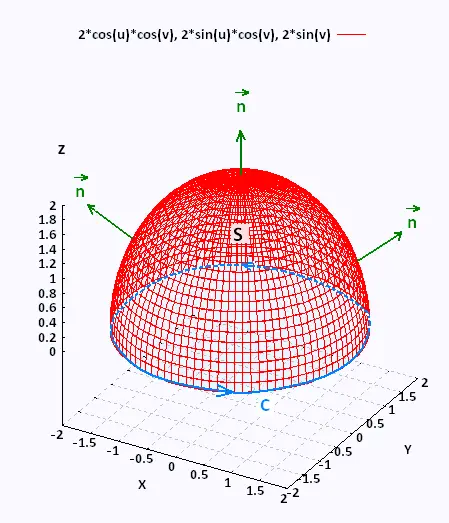
Lets's consider the following surface with the indicated orientation ,
delimited by the oriented contour C.
This curve C, around the edge of the surface S is called the boundary curve.
The orientation of the surface S induces the positive orientation of C. To
determine the positive orientation of C related to the orientation of the
unit normal vector, we use the right-hand rule, or think of walking
along the curve, while the surface is on the left, so the direction of the unit
normal vectors is upwards.
2. Stokes� Theorem
Here is Stokes' theorem:
S is any oriented smooth surface that is bounded by a simple,
closed, smooth boundary curve C with positive orientation.
 is a vector field: is a vector field:
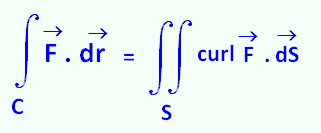
Example 1
Evaluate ∫∫S curl( ) . ) .  by using Stokes� Theorem.
by using Stokes� Theorem.
where  =
xy =
xy  +
y +
y  ,
and S is the part of z = 6 - x2 - y2 above the plane
z = 2 . ,
and S is the part of z = 6 - x2 - y2 above the plane
z = 2 .
Consider that S is oriented upwards.
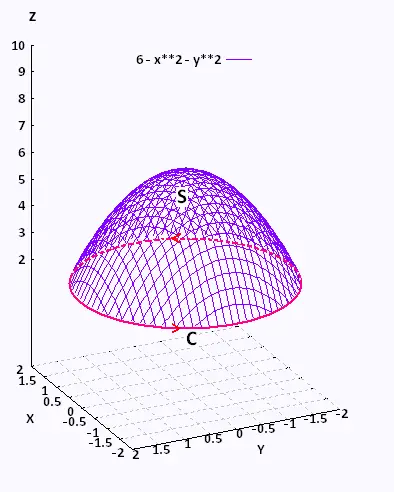
The boundary curve C is the intersection of the surface S and the
plane z = 2. So
6 - x2 - y2 = 2. That is:
x2 + y2 = 4, at z = 2.
Therefore, the boundary curve C of S is the circle of radius 2, centred
at the origin on the plane z = 2. The parameterization of this curve S is:
 (t) = 2 cos t (t) = 2 cos t  + 2 sin t + 2 sin t  + 2 + 2  ,
with
0 ≤ t ≤ 2π . ,
with
0 ≤ t ≤ 2π .
The vector field evaluated on the curve is:
 ( ( (t)) =
4 sin t cos t (t)) =
4 sin t cos t  +
0 +
0  +
2 sin t +
2 sin t 
We have :
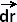 /dt =
- 2 sin t /dt =
- 2 sin t  + 2 cos t + 2 cos t 
and dr = (dr/dt) dt. Then
∫c  . . 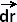 =
∫02π =
∫02π  ( ( (t)). ( (t)). (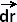 /dt) dt = /dt) dt =
∫02π
〈 4 sin t cos t , 0 , 2 sin t 〉 . 〈 - 2 sin t , 2 cos t , 0 〉 dt
=
∫02π
(- 8 sin2 t) dt
=
(- 4) ∫02π
(1 - cos (2t)) dt =
(- 4) ∫02π
(t - (1/2) sin (2t)) dt = - 8 π
∫c  . . 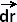 = - 8 π
= - 8 π
Example 2
Evaluate ∫C  . . 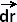 by using Stokes� Theorem.
by using Stokes� Theorem.
where  =
z2 =
z2  +
y +
y  +
z +
z  , ,
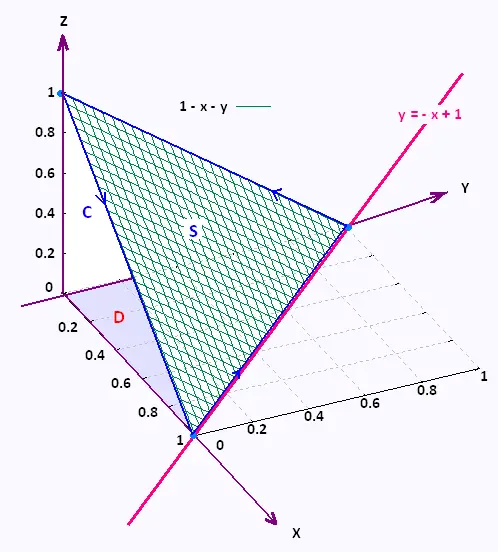
C is the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1)
with counter-clockwise rotation. .
curl  = = |
 |
 |
 |
 |
 |
| ∂/∂x
|
∂/∂y
|
∂/∂z
|
| z2
|
y
|
z
|
= 〈 0, 2z, 0 〉 = 2z  . .
The triangle C is the boundary curve for the surface S that we need
to use in the surface integral. S is any surface that
has this boundary. So Let�s use the plane formed by the
triangle, with upwards orientation for this surface.
The equation of this plane S is :
x + y + z = 1 . or z = g(x,y) = 1 - x - y.
The related function of the surface f is:
f(x,y,z) = 0 = x + y + z - 1. Hence
∇f = 〈 1, 1, 1 〉
The region D over we integrate is bouded by
0 ≤ x ≤ 1 and 0 ≤ y≤ 1 - x
Let�s use Stokes� Theorem :
∫C  . . 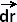 =
∫∫S curl( =
∫∫S curl( ) . ) . 
∫∫S curl( ) . ) .  = =
∫∫S 2z  . .  dS =
∫∫S 2z dS =
∫∫S 2z  . (∇f/|∇f|) dS = . (∇f/|∇f|) dS =
∫∫D 2z  . ∇f dA =
∫∫D 2z 〈 0, 1, 0 〉 . 〈 1, 1, 1 〉 dA = . ∇f dA =
∫∫D 2z 〈 0, 1, 0 〉 . 〈 1, 1, 1 〉 dA =
∫∫D 2z dA =
∫0 1
∫01-x
2(1 - x - y) dy dx
=
2∫0 1
(y - xy - y2/2) |01-x
dx
=
2∫0 1
(1/2)(1 - x )2 dx
=
∫0 1 (1 - x )2 dx
=
- (1/3) (1 - x )3|0 1 = 1/3
∫c  . . 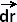 = 1/3
= 1/3
|
|