Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Parametric surfaces
1. Definitions and method
We have seen that the parameterization of a curve consists in
taking values of t from an interval [a, b] and substitute them into
the vector function :
 (t) =
x(t) (t) =
x(t)  +
y(t) +
y(t)  + z(t) + z(t) 
The resulting set of vectors is the position vectors for the points on the curve.
The parameterization of surfaces is similar.
We take two points (u, v) out of a two-dimensional
space D and substitute them into
the vector function
 (u,v) =
x(u,v) (u,v) =
x(u,v)  +
y(u,v) +
y(u,v)  + z(u,v) + z(u,v) 
The resulting set of vectors is the position vectors for the points on the surface S to parameterize.
The vector  (u,v) is called the parametric representation of the parametric surface S. (u,v) is called the parametric representation of the parametric surface S.
The parametric equations for a surface are the components of the parametric representation:
x = x(u,v) , y = y(u,v), z = z(u,v)
Example 1
Determine the surface given by the following parametric representation:
 (u,v) =
u cos v (u,v) =
u cos v  +
u sin v +
u sin v  + u + u 
The parametric equations are:
x = u cos v , y = u sin v, z = u
Let's square x, y and z ; we obtain:
z2 = x2 + y2
We have then eliminated the parameters to obtain an equation
in x, y, and z. This quadric surface is a cone
open along the z-axis.
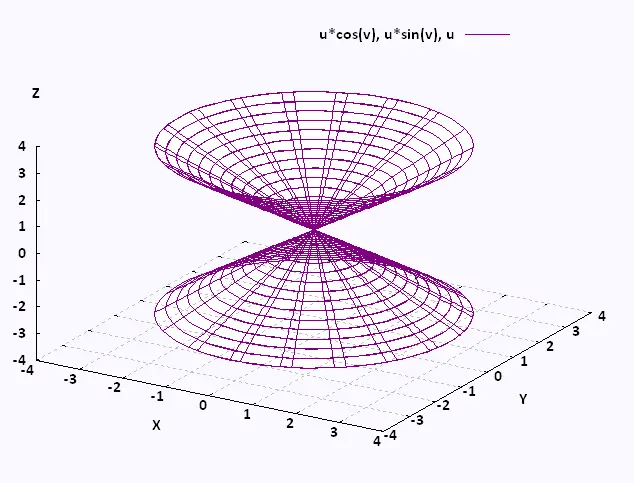
Example 2 : Sphere
Give a parametric representation of the surface:
x2 + y2 + z2 = 16
Converting Cartesian coordinates into spherical coordinates gives
the parametric representation:
 (θ,φ) =
4 sin θ cos φ (θ,φ) =
4 sin θ cos φ  +
4 sin θ sin φ +
4 sin θ sin φ  + 4 cos θ + 4 cos θ 
With the two restrictions:
0 ≤ θ ≤ π and 0 ≤ φ ≤ 2π
Example 3 : Cylinder
Give a parametric representation of the surface:
x2 + y2 = 16
Converting Cartesian coordinates into cylindrical coordinates gives
the parametric representation:
 (z,θ) =
4 sin θ (z,θ) =
4 sin θ  +
4 cos θ +
4 cos θ  + z + z 
With the restriction:
0 ≤ θ 2π
Example 4 : Elliptic paraboloid
Give a parametric representation of the surface:
y = 2x2 + 3z2 - 16
The surface is in the form y = f(x, z). So x and z becomes parameters:.
So the parametric equations are:
x = x , z = z , y = 2x2 + 3z2 - 16
The parametric representation is then:
 (x, z) =
x (x, z) =
x  +
(x2 + 3z2 - 16 ) +
(x2 + 3z2 - 16 ) + z + z 
Note that, in the same manner, we can have:  (x, y),
or (x, y),
or  (y, z) (y, z)
Application: tangent plane to the parametric
surface S
Find the tangent plane to the parametric surface S given by:
 (u,v) =
x(u,v) (u,v) =
x(u,v)  +
y(u,v) +
y(u,v)  + z(u,v) + z(u,v) 
Let's determine the partial derivatives of this
parametric representation :
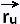 (u,v) = (u,v) =
(∂x(u,v)/∂u)  +
(∂y(u,v)/∂u) +
(∂y(u,v)/∂u)  + (∂z(u,v)/∂u) + (∂z(u,v)/∂u)
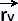 (u,v) = (u,v) =
(∂x(u,v)/∂v)  +
(∂y(u,v)/∂v) +
(∂y(u,v)/∂v)  + (∂z(u,v)/∂v) + (∂z(u,v)/∂v)
The non-zero vector cross product 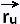 (u,v) x (u,v) x 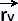 (u,v) is orthogonal to the
surface S, then normal to the tangent plane to this surface. (u,v) is orthogonal to the
surface S, then normal to the tangent plane to this surface.
Example 5
Find the tangent plane to the parametric surface S given by:
 (u,v) =
u (u,v) =
u  +
v2 +
v2  + (u2 + v) + (u2 + v)
at the point P (- 1, 1, 0)
The partial derivatives are:
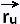 (u,v) = (u,v) =
 + 2u
+ 2u 
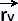 (u,v) =
2v (u,v) =
2v  + + 
The cross product gives the normal vector  : :
 = = 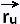 (u,v) x (u,v) x 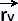 (u,v) = 〈 - 4uv, - 1, 2v 〉 (u,v) = 〈 - 4uv, - 1, 2v 〉
Now, we determine the value of u and v at the point P :
To do this, we set the components of the parametric representation equal to the coordinates of the point (- 1, 1, 0). That is:
u = - 1
v2 = 1 → v = - 1 or v = + 1
u2 + v = 0 → v = - 1
Hence the correct values are :
u = - 1 , and
v = - 1
Substituting these two values in, the normal vector becomes:
 = = 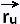 (u,v) x (u,v) x 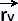 (u,v) = 〈 - 4 , - 1, - 2 〉 (u,v) = 〈 - 4 , - 1, - 2 〉
Therefore, the equation of the tangent plane is:
M(x, y, z), P (- 1, 1, 0) , so 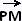 = 〈 x + 1, y - 1, 0 - z 〉 = 〈 x + 1, y - 1, 0 - z 〉
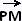 . .  = 0 = 0
〈 x + 1, y - 1, 0 - z 〉 . 〈 - 4 , - 1, - 2 〉 = 0
- 4(x + 1) - 1(y - 1) - 2(0 - z) = 0
- 4 x - y + 2 z - 3 = 0
|
|