Calculus III:

functions of more than one variable
Functions of two variables
Domains and graphs

1. Domain of functions

The domain of a function of more than one variable is similar to that on variable.

For a single variable function, y = f(x), the domain is the set that contains all the values of x that we could substitute in the function and get back a real number. This domain is an interval (or intervals) of values from the number line, or one dimensional space.

For a multiple variable function, y = f(x,y,..), the domain is the set that contains all the values of x, y, ... that we could substitute in the function and get back a real number.

For a two variable function, y = f(x,y), the domain is the set that contains all the values of the couple (x,y) that we could substitute in the function and get back a real number. This domain is a two dimensional space .

2. Graphs of functions of two variables

The graphs of functions of two variables, z = f(x,y) are surfaces in three dimensional space.

Example 1

The graph of the plane z = f(x,y) = - x - y + 1:



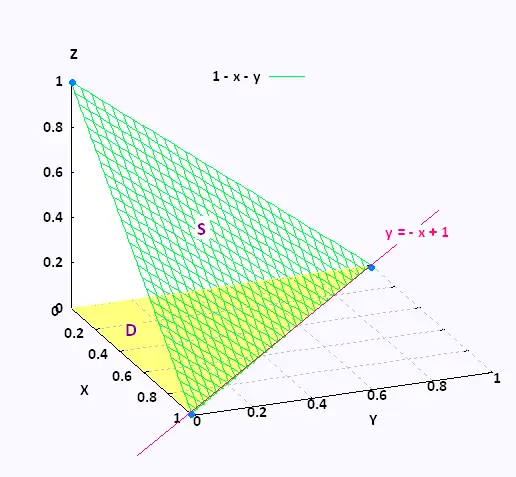
The surface is a triangle, partion of the plane x + y + z = 1, formed by the vertices (0,1,0), (1,0,0), and (0,0,1) that lies in the first octant.

Example 2

The graph of z = 8 - 2 x² - 2 y².



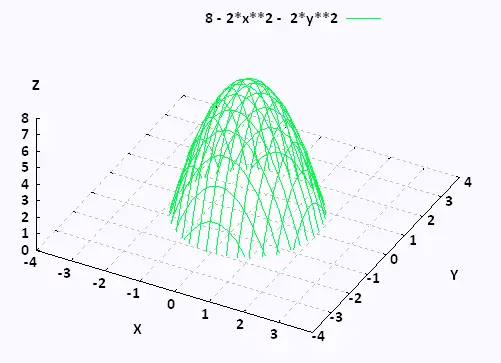
This is an elliptic parabaloid and is an example of a quadric surface.

3. Level curves of a surface

The level curves are called contour curves. The level curves of the function z = f(x,y) are the curves we get by setting z = k , k is a constant number. These curves are then two dimentional or plane. So



The equations of the level curves are z = f(x,y) = k.

Note that the equation f(x,y) = k can be written in the form f(x,y) - k = 0, so the equation of the level curve becomes g(x,y,z) = 0.

Example 1

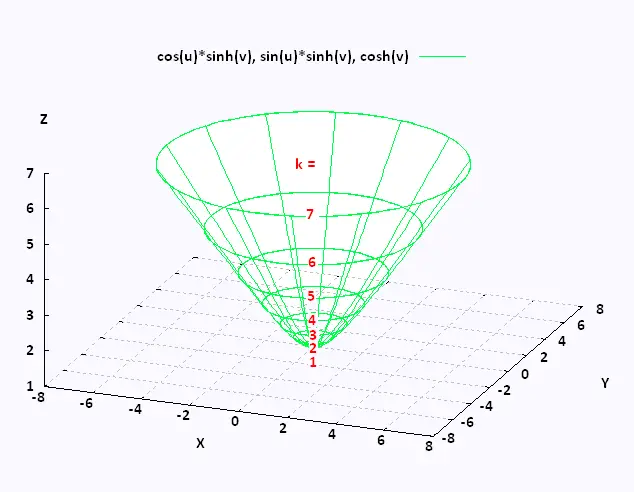
We want to identify some levels of the curves of z = f(x,y) = √[x² + y²] which is the upper half of a cone.

The level curves (or contour curves) for this surface are given by the equation z = k , that is x² + y² = k ² .

So, the level curves are circles of radius k centered at the origin.

Here seven level curves corresponding to k = 1, 2, 3, 4, 5, 6, and 7.

The contours represent the intersection of the surface that is given by z = f(x,y) and the plane z = k.

The levels of z = f(x,y) are the levels of the function f(x,y,z) = z - √[x² + y²] = 0

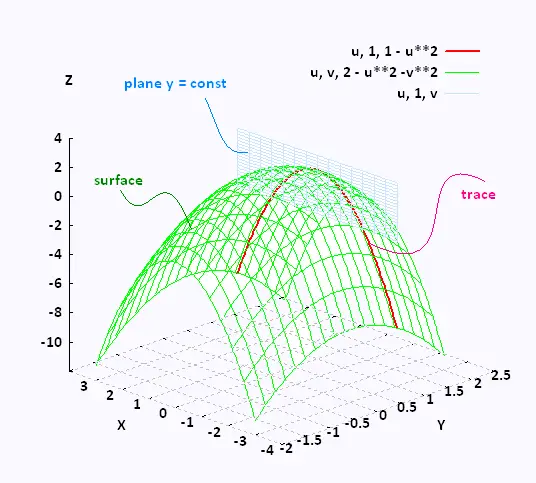
4. Traces of surface

The contours is the intersection of the surface given by z = f(x,y) and the plane z = k .

Traces of surfaces are curves that represent the intersection of the surface and the plane given by x = k or y = k .

Example

Here is an example that shows the trace of the surface given by z = f(x,y) = 2 - x² - y² at y = 2.

This trace is all the points in the intersection of the surface and the plane y = 2.