Calculus III:

Integrals
Change of variables
Jacobian of a transformation

1. Definitions

The substitution rule in integral:

∫_a^b f(g(x)) dg(x) = ∫_c^d f(u) du
where
dg(x) = g'(x) dx and u = g(x)

used in one-dimension holds in two-dimensions and three-dimensions integrals.

For a function, the set of equations u = g(x) that define the change of variables are called the transformation .

The change of variables is maily used to get the related calculus easier. For example converting double integrals to polar coordinates or triple integrals to cylindrical or spherical coordinates.

The change of variables in integrals involve the conversion of the region, over we integrate, the fonction itself, and the differential element.

2. Examples: Change in the region of integration :
xy-coordinates → uv-coordinates

Example 1

The region R, over we want to integrate, is an ellipse defined by x² + y²/16 = 1.

We want to determine the new region of R due to the given transformation x = u/2 and y = 2v.

Substituting x anf y in the equation yields:

u²/4 + v²/4 = 1

u² + v² = 4

This change of variables transforme the ellipse to a disk of radius 2.

Example 2

The region R, over we want to integrate, is a triangle delimited by the three lines y = - x + 1, y = 2x - 2, and y = x + 1.



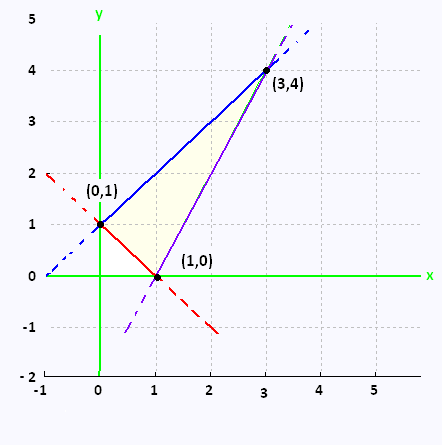
We want to determine the new region of R due to the given transformation x = (u + v)/2 and y = (u - v)/2 .

Substituting x anf y in the three equations yields:

y = - x + 1
(u - v)/2 = - (u + v/2 + 1
u - v = - u - v + 2
u = 1

y = 2x - 2
(u - v)/2 = (u + v) - 2
u - v = 2u + 2v - 4
u + 3 v = 4
v = - u/3 + 4/3

y = x + 1.
(u - v)/2 = (u + v)/2 + 1
u - v = u + v + 2
v = - 1

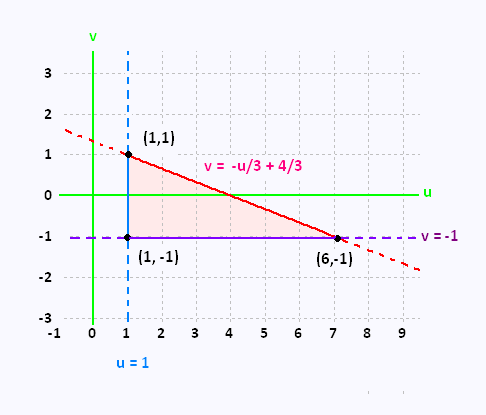
This change of variables transform the triangle to a right triangle .

3. Jacobian of the differential element

3.1. Double integral

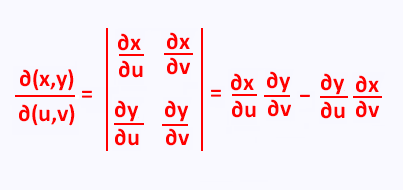
The Jacobian of the transformation:
x = g(u,v)
y = h(u,v)

is:

The change of variables for a double integral over the region R, under the transformation x = g(u,v) , y = h(u,v), becomes the integral over S as follows:


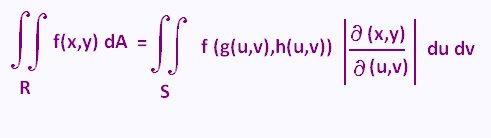
Notice that, now, we are integrating with respect to u and v. Also note that we are taking the absolute value of the Jacobian.

The relationship between the differentials dA and du dv is :

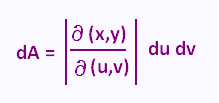
Example 3:

Show that the changing from the cartesian coordinates to polar coordinates is dA = r dr dθ.

The transformation is : x = r cos θ , y = r sin θ .

u = r
v = θ

∂x/∂u = cos θ
∂x/∂v = - r sin θ

∂y/∂u = sin θ
∂y/∂v = r cos θ

The Jacobian for this transformation is :

(cos θ)(r cos θ) - (sin θ)(- r sin θ) = r cos² θ + r sin² θ = r

Therefore

dA = Jacobian dr dθ = r dr dθ

The differential element in polar coordinates is : dA = r dr dθ

Example 4

The region R, over we want to integrate, is a trapezoidal region having the four vertices (0,0), (2,2), (2, -2) and (4,0).

The related lines have the equations: y = x , y = - x , y = x - 4 , and y = - x + 4



a) Determine the new region of R due to the given transformation x = 2u - 3v and y = 2u + 3v .

b) Evaluate ∫∫_R (x - y) dA

a) Substituting x anf y in the three equations yields:

y = x → 2u + 3v = 2u - 3v → v = 0
y = - x → 2u + 3v = - 2u + 3v → u = 0
y = x - 4 → 2u + 3v = 2u - 3v - 4 → v = 2/3
y = - x + 4 → 2u + 3v = - 2u + 3v + 4 → u = 1

This change of variables transform the trapezoidal region to a rectangle.



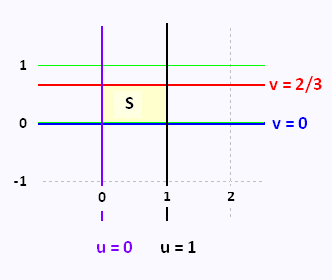
∂x/∂u = 2
∂x/∂v = - 3

∂y/∂u = 2
∂y/∂v = 3

The Jacobian for this transformation is :

(3)(3) - (2)(- 3) = 9 + 6 = 15

The differential element becomes: dA = 15 du dv

b) Here are the limits of integration:

0 ≤ u ≤ 1
0 ≤ v ≤ 2/3

∫∫_R f(x,y) dA = ∫∫_S 15 f(u,v) du dv

∫∫_R (x - y) dA = ∫∫_S 15 [(2u - 3v) - (2u + 3v)] du dv =

∫∫_S 15 (- 6 v) du dv = ∫∫_S 15 (- 6 v) du dv =

- 90 ∫₀^2/3 ∫₀¹ v du dv = - 90 ∫₀^2/3 (1) v dv =

- 90 (1) ((2/3)²/2) = - 90 (4/9) (1/2) = - 20

∫∫_R f(x,y) dA = - 20

Example 5

Evaluate ∫∫_R x² - xy + y² dA, where R is the ellipse of equation x² - xy + y² = 4, and using the transformation:

x = u - v/√3
y = u + v/√3

First, we transforme first f(x,y) = x² - xy + y².

x² - xy + y² = (x - y)² + xy = (- 2v/√3)² + (u - v/√3)(u + v/√3) =

4v²/3 + u² - (v/√3)² = 4v²/3 + u² - v²/3 = u² + v²

x² - xy + y² = u² + v²

R is transformed into a circle of radius r = 2.

∂x/∂u = 1
∂x/∂v = - 1/√3

∂y/∂u = 1
∂y/∂v = 1/√3

The Jacobian for this transformation is :

(1)(1/√3) - (1)(- 1/√3) = 2/√3.

The differential element becomes:

dA = (2/√3) du dv

Therefore, the integral becomes:

∫∫_R x² - xy + y² dA = ∫∫_S u² + v² (2/√3) du dv

The second change into polar coordinates u r cos θ v = r sin θ leads to:

∫∫_S r² (2/√3) r dr dθ = ∫₀^2π ∫₀² r³ (2/√3) dθ =

∫₀^2π (2⁴/4) (2/√3) dθ = (2⁴/4) (2/√3) 2π = 16 π/√3

∫∫_R x² - xy + y² dA = 16 π/√3

3.2. Triple integral

We will use the transformation x = g(u,v,w), h(u,v,w), k(u,v,w) , and transform the region R into the new region S.

To do the integral, we will need a Jacobian. Here is the definition of the Jacobian in three-dimentional space for this transformation.



The change of variables for a triple integral over the region R, under the transformation x = g(u,v,w), y = h(u,v,w), z = k(u,v,w) , becomes the integral over S as follows:



Notice that, now, we are integrating with respect to u , v, and w. Also note that we are taking the absolute value of the Jacobian.

The relationship between the differentials dV and du dv dw is :



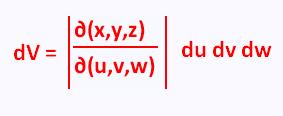
The transformation is : x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ.

u = r
v = θ
w = φ

∂x/∂u = sin θ cos φ
∂x/∂v = r cos θ cos φ
∂x/∂w = - r sin θ sin φ

∂y/∂u = sin θ sin φ
∂y/∂v = r cosθ sin φ
∂y/∂v = r sin θ cos φ

∂z/∂u = cos θ
∂z/∂v = - r sin θ
∂z/∂v = 0

The Jacobian for this transformation is :

sin θ cos φ	r cos θ cos φ	- r sin θ sin φ
sin θ sin φ	r cosθ sin φ	r sin θ cos φ
cos θ	- r sin θ	0

=

(sin θ cos φ)[(0) - (r sin θ cos φ)(- r sin θ )] +
(r cos θ cos φ )[( r sin θ cos φ )(cos θ ) - (0)] +
(- r sin θ sin φ )[(sin θ sin φ)(- r sin θ ) - (cos θ)(r cosθ sin φ )] =

r² sin θ cos φ sin² θ cos φ + r² cos² θ cos² φ sin θ +
(r² sin θ sin² φ ) [sin² θ + cos² θ] =

r² sin θ[ cos² φ (sin² θ + cos² θ ) + sin² φ ] =

r² sin θ[ cos² φ + sin² φ ] = r² sin θ

Then

Jacobian = r² sin θ

Therefore

dA = Jacobian . dr dθ dφ = r² sin θ dr dθ dφ

The differential element in spherical coordinates is : dA = r² sin θ dr dθ dφ