Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
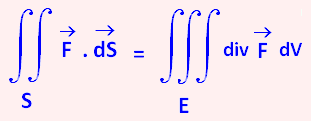
Divergence theorem
Green’s Theorem relates line integral to double integral over a region
delimited by an oriented curve.
Stokes' theorem relates
a line integral to surface integral over a region
delimited by an oriented curve.
Divergence theorem relates surface integral to triple integral over a region
delimited by an oriented surface.
Divergence theorem
E is a simple solide reigion . S is the boundary surface of E
with positive orientation.  is a vector
field with continuous first order partial derivatives components:
Example
Use the divergence theorem to evaluate
∫∫S .  ,
where:
=
xy  +
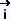xz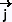 
(3 - y)z  ,
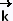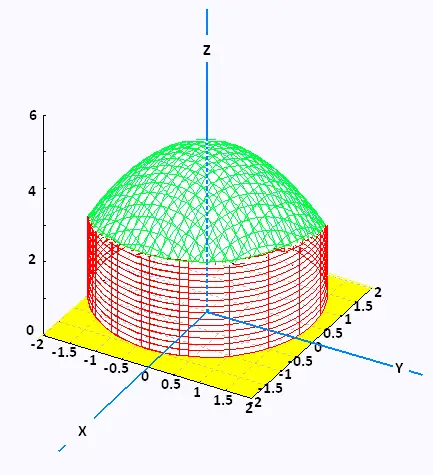
and the surface S is a wrapped dome, that has three parts:
. On the top: paraboloid z = 10 - 2 x2 - 2 y2 , 2 ≤ z ≤ 10
. On the side: Cylinder x2 + y2 = 4 , 0 ≤ z ≤ 2
. On the bottom: disk x2 + y2 = 4 , z = 0
∫∫S . =
∫∫∫E div dV
.
Let's work on ∫∫∫E div dV.
The region E for the triple integral is then the solid enclosed by these
three surfaces.
The cylindrical coordinates system is the appropriate system
for this region:
x = r cos θ
y = r sin θ
z = 10 - 2 r2cos2 θ - 2 r2 sin2 θ =
10 - 2 r2
The limits for the ranges are:
0 ≤ r ≤ 2
0 ≤ θ ≤ 2π
0 ≤ z ≤ 10 - 2 r2
We have:
dV = r dr dθ dz.
= 〈xy , xz , (3 - y)z 〉. Hence
div = y + 0 + 3 - y = 3
div = 3.
Therefore
∫∫∫E div dV =
∫02π
∫02
∫010 - 2 r2 3 dz r dr dθ =
3 ∫02π
∫02
(10 - 2 r2) r dr dθ =
6 ∫02π
((5/2) r2 - (1/3)r3)|02 dθ =
6 ∫02π
((10 - 8/3) dθ =
44 ∫02π
dθ =
88 π
∫∫S . =
∫∫∫E div dV =
88 π
|
  |
