Calculus III: parametric equations
Cycloid

1. Parametric equations for the cycloid

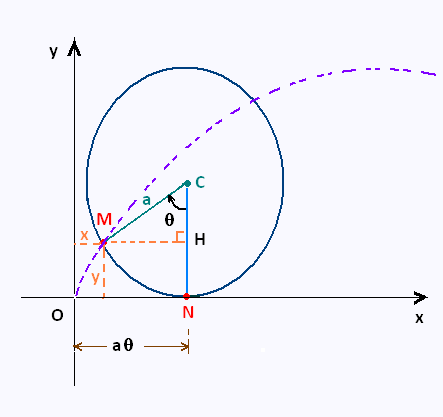
A cycloid is the curve traced by a point on a circle as it rolls along a straight line.

NM = ON

A moving point on the circle goes from O(0,0) to M(x,y). It describes the arc NM of length equal to a θ .

The coordinates x and y of the point M are:

x = ON - MH = aθ - a sin θ
y = CN - CH = a - a cos θ

so the parametric equations for the cycloid are:

x = a (θ - sin θ)
y = a(1 - cos θ)

1.1. Area under an arch of a cycloid

The the parametric equations of the cycloid , we get the corresponding derivatives :

dx = a (dθ - cos θ dθ)
dy = a sin θ dθ

with 0 ≤ θ ≤ 2π

The area under the arch is:

∫₀^2π y dx = ∫₀^2π a(1 - cos θ) a (dθ - cos θ dθ) =
a² ∫₀^2π (1 - cos θ)² dθ =
a² ∫₀^2π ((3/2)θ - 2 sin θ + (1/2) sin θ cos θ) dθ = 3 π a²

so the area under an arch is:

A = 3 π a²

1.2. Arch length of the cycloid

S = ∫₀^2π [(dx/dθ)² + (dy/dθ)²]^1/2 dθ =
= ∫₀^2π a[2 - 2 cos θ]^1/2 dθ = = ∫₀^2π 2a |sin(θ/2)| dθ =
= 2∫₀^π 2a sin(θ/2) dθ = 8 a

so the arc length of one arch of a cycloid is:

S = 8 a

2. The inverted cycloid

Rotated through 180^o, we get the inverted cycloid, an intersting curbe in Physics.

The inverted cycloid is the curve of fastest descent under gravity. We can prove this by using the Lagrangian formalism.