Calculus III:

Cylindrical coodinates system
The volume element in cylindrical coordinates
Triple integrals in cylindrical coordinates

1. Cylindrical coodinates system

In 3D space, the standard coordinate system, is the Cartesian coordinate system (x, y, z).

An alternate coordinate system for three dimensional space is the cylindrical coodinates system

The cylindrical coodinates system is an extension of polar coordinates into three dimensions by adding z as the third coordinate. The r and θ are the same as with polar coordinates.



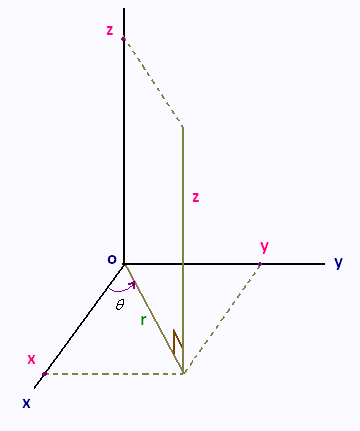
For a point in cylindrical coordinates the cartesian coordinates can be found by using the following conversions.

x = r cos θ
y = r sin θ
z = z

As for the 2D polar system, we have still the following conversions:

r² = x² + y², and tan (θ) = y/x

2. Volume element in cylindrical coordinates

The volume element in cylindrical coordinates comes from the area element in polar coordinates times the height dz. That is: dV = r dr dθ dz

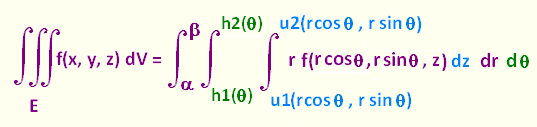
3. Triple integral in cylindrical coordinates

With D being the region in the xy-plane, the region E over which we integrate is:

E = {(x, y, z) | (x, y) ∈ D, u1(x,y) ≤ z ≤ u2(x,y)}

E = {(r, θ, z) | α ≤ θ ≤ β, h1(θ) ≤ r ≤ h2(θ),
u1(r cos θ, r sin θ) ≤ z ≤ u2(r cos θ, r sin θ)}

The triple integral in the cylindrical coordinates is:

4. Examples

Example 1

Find ∫∫∫_E x dV, where E is the region that lies below the plane z = x + 3 above the xy-plane and between the cylinders x² + y² = 1 and x² + y² = 9.

We convert and integrate:

Because z is above the xy-plane so z ≥ 0 .

0 ≤ z ≤ x + 3 → 0 ≤ z ≤ r cos θ + 3

The region D is the region between the two circles x² + y² = 1 and x² + y² = 9 ,
then the ranges for D is:

0 ≤ θ ≤ 2π , 1 ≤ r ≤ 3

The triple integral is:

∫∫∫_E x dV = ∫₀^2π ∫₁³ ∫₀^{r cos θ + 3} r² cos θ dz dr dθ

Example 2

Convert
∫- 1+1 ∫0√(1 - y2) ∫x2 + y2√(x2 + y2) x y z dz dx dy
into an integral in cylindrical coordinates.

The ranges of the variables x, y, and from this iterated integral are:

- 1 ≤ y ≤ +1
0 ≤ x ≤ √(1 - y²)
x² + y² ≤ z ≤ √(x² + y²)

The first two inequalities define the region D. Since x ≥ 0 , and - 1 ≤ y ≤ +1 , D is reduced to the right half a circle of radius 1 centered at the origin.

So, the ranges for D in cylindrical coordinates are:

0 ≤ r ≤ 1
- π/2 ≤ θ ≤ +π/2
r² ≤ z ≤ r

Therefore, the integral is:

∫- 1+1 ∫0√(1 - y2) ∫x2 + y2√(x2 + y2) x y z dz dx dy =
∫- π/2+π/2 ∫01 ∫r2 r z r3 cos θ sin θ dz dr dθ