Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Equation of a line in 3D space
Vector form of the equation of a line
Parametric form of the equation of a line
Symmetric equations of the line
1. Equation of a line in 3D space
1. Vector form of the equation of a line
We know already that the graph of a line in 3D space us aplane.
In this section we need to determine and write down the equation of a line in 3D space R3.
In two dimensions space R2, we need the slope (p) and a point on the line in order to write down the equation y = p x + q.
In 3D space R3, the equation is vectorial . That is:
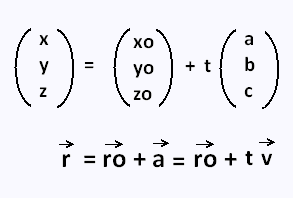
This form of the equation of the line in 3D space est called
the
vector form of the equation of a line .
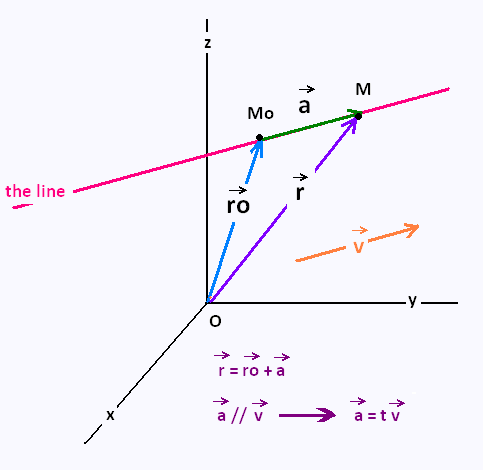
• (x,y,z) are the coordinates, in 3D space, of any point on the line. They are also the coordinates of any position vector r
• (xo,yo,zo) are the coordinates of a known point on the line. They are also the coordinates of the position vector ro
• (a,b,c) are the coordinates of the vector-slope v which is parallell vector to the line, (to the vector a). This vector can be on the line or outside the line. It does not need to be a position vector, and
• t is a real parameter. It tells us that if t > 0 , the point M moves toward the right, and if t < 0 ,
the point M moves towards the left. As t varies over all possible values, we will completely cover the line.
2. Parametric form of the equation of a line
If we develop the vectorial form and equatomg
the components,
we get:
x = xo + t a
y = yo + t b
z = zo + t c
Which is called the parametric form of the equation of a line
From a taken value of t, we get a position vector in the vector form of the line for the point and in the parametric form we get the actual coordinates of the point.
3. Symmetric equations of the line
The parametric form can be written as
x - xo = t a
y - yo = t b
z - zo = t c
By combining and rearranging those three equations,
we
obtain:
(x - xo)/ a = (y - yo)/b = (z - zo)/c = t
Therefore, with a, b, and c non equal to zero, the equation
of the line in 3D space can take the following form:
(x - xo)/ a = (y - yo)/ b = (z - zo)/c
Which is called symmetric equations of the line.
Remark that if one of the components a, or b, or c is equal to zero, we solve the parametric equations for non the zero parameters.
For exemple :
If a = 0, then
x = xo
(y - yo)/ b = (z - zo)/c
2. Exemples
Example 1
Write down the equation of the line that passes through
the points and Po(1,- 2,4) and P1(5,- 5,6) .
The vector v that is parallel to the line is:
v = P2Po = (4, - 3, 2)
We have two known points, we can use either one.
We take the first Po.
The vector form of the equation of a line is
(x,y,z) = (1, -2,4) + t(4, - 3, 2)
The parametric form of the equation is:
x - 1 = 4 t
y + 2 = - 3 t
z - 4 = 2 t
The symmetric equations of the line is
(x - 1)/ 4 = - (y + 2)/3 = (z - 4)/2
Example 2
The line (d1) passes through the point (- 1,5, 0) and is
parallel to the line (d2) given by its parametric form :
x = 1 + 2 t
y = 3 - 5 t
z = 4 t
We ask to determine whether the line (d1) passes through
the xz-plane. If it does give the coordinates of that point.
Solution:
The vector v that is parallel to the line (d2) is:
v = (2, - 5, 4)
Also, this vector is parallel to (d1). So the parametric equation
of the line (d1) is:
x = - 1 + 2 t
y = 5 - 5 t
z = 0 + 4 t
If the line (d1) passes through the xz-plane, then
at that
crossing point, we must have y = 0 . That is 5 - 5t = 0
Hence t = 1 .
We have solved for t, therefore the line does pass through
the xz-plane. So the coordinates of the point where (d1) passes
through the xz-plane are:
(1, 0, 4)
|
|