Calculus III:

Polar coodinates system
Polar Coordinates
The area element in polar coordinates
Double integrals in polar coordinates

1. Polar coodinates system

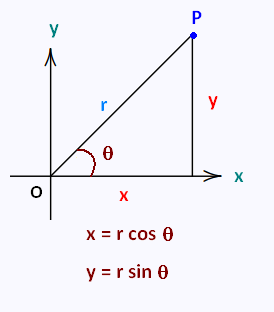
The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.

The reference point (O) is analogous to the origin of a cartesian system. It is called the pole. The ray from the pole in the reference direction (x-axis) is the polar axis. The distance from the pole to a point(x,y) is called the radial coordinate or radius (r), and the angle (θ) is the angular coordinate, polar angle, or azimuth.

Polar coordinates are a different way of describing points in the plane. The polar coordinates (r, θ) are related to the usual rectangular coordinates (x, y) by

x = r cos θ, y = r sinθ

The related equations are:

r² = x² + y²,
tan(θ) = y/x

2. The area element in polar coordinates

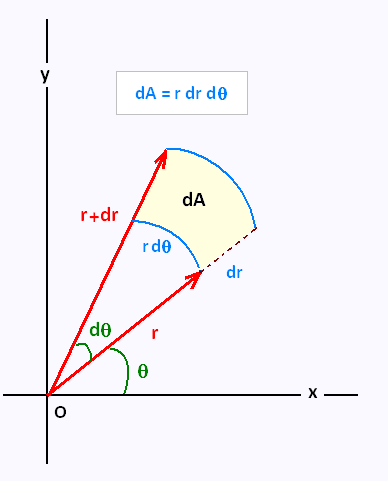
In polar coordinates the area element is: dA = r dr dθ.

3. Double integrals in polar coordinates

Double Integrals Over General Regions need to determine the region D over to integrate . In the case of this region D is somewhat circular, using polar coordinates , double integrals are is more easily described.

For instance, a region that is a disk, ring, or a portion of a disk or ring. In these cases using Cartesian coordinates could be somewhat cumbersome.

Let's consider the following integral:

∫∫_D f(x,y) dA , where D is a circle of radius 3. So
D = {(x,y)| - 3 ≤ x ; ≤ + 3, - √(9 - x²) ≤ y ≤ +√(9 - x²)}

∫∫D f(x,y) dA = ∫-3+3 ∫- √(9 - x2 √(9 - x2 f(x,y)dy dx

The inner integral involving these limits asks a lot of work to compute.

However, a disk of radius 3 can be defined in polar coordinates by the following simple inequalities:

0 ≤ r ≤ 3, 0 ≤ y ≤ 2π.

So the intagral becomes easier to compute:

∫∫_D f(x,y) dA = ∫₀³ ∫₀ ^2π f(rcosθ,rsinθ)rdr dθ

5. General region in polar coordinates

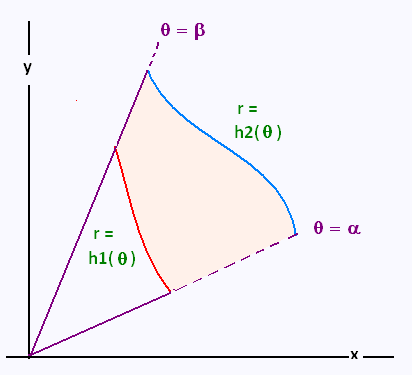
The general region is defined by the two inequalities:

α ≤ θ ≤ β, h1(θ) ≤ r ≤ h2(θ)

We have then the formula:

5. Examples

Examples 1

Find the integral ∫∫_D 3x y dx dy by converting it into polar coordinates.
D is the portion of the region between the circles of radius 1 and radius 4 centered at the origin that lies in the first quadrant.

The region is defined by the two inequalities:

0 ≤ θ ≤ π/2, 1 ≤ r ≤ 4

∫∫_D 3x y dx dy =
∫₀^π/2 ∫₁⁴ 3 r³ cos θ sin θ dr dθ =
∫₀^π/2 (3/4) r⁴|₁⁴ cos θ sin θ dθ =
∫₀^π/2 (3/4)(255) cos θ sin θ dθ =
(3/4)(255)∫₀^π/2(1/4)sin(2θ)d(2θ) =
(1/4)(3/4)(255) (- cos 2θ))|₀^π/2 =
(1/4)(3/4)(255)(1 + 1) =
(3/8)(255) = 765/3

∫∫_D 3x y dx dy = 765/3

Examples 2

Find the integral ∫∫_D exp{x² + y²}dA .
D is the unit circle centered at the origin.

∫∫_D exp{x² + y²} dA =
∫∫_D exp{x² + y²} dx dy =
∫₀^2π ∫₀¹ exp{r²sin²θ + r²cos² θ} r dr dθ =
∫₀^2π ∫₀¹ exp{r²} r dr dθ = (1/2) ∫₀^2π exp{r²}|₀¹ dθ =
(1/2) ∫₀^2π (e - 1) dθ =
(1/2)(e - 1) (θ)|₀^2π = π(e - 1)

∫∫_D exp {x² + y²} dA = (e - 1)π

Examples 3

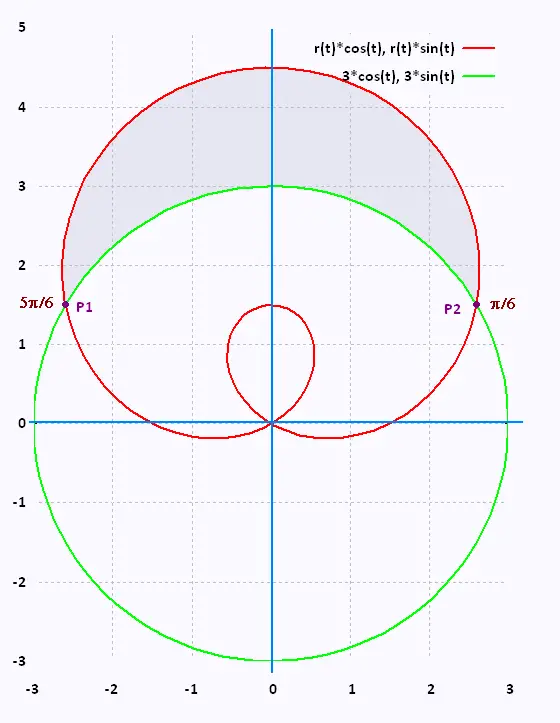
By Gnuplot:
reset
set grid
set parametric
r(t) = 1.5 + 3sin(t)
plot [0:2*pi] r(t)*cos(t), r(t)*sin(t), 3*cos(t), 3*sin(t)

We want to retermine the area of the region that lies inside 1.5 + 3sin(θ) and outside r = 3.

We need first to determine the angles of the two points of intersection P1 and P2.

They are given by equationg the two equations :

r(θ) = 1.5 + 3sin(θ ), and r(θ) = 3 . So

1.5 + 3sin(θ ) = 3 → sin(θ) = 1/2

Recall:
sin (x ) = a
x = arcsin (a) + 2kπ
x = π - arcsin (a) + 2kπ
k ..., -2, -1 , 0, 1, 2, , ...

Then

θ = π/6
θ = π - π/6 = 5π/6

Therefore

∫∫_D dA = ∫∫_D dx dy =

∫_π/6^5π/6 ∫₃^{1.5 + 3sin(θ)} r dr dθ =

∫_π/6^5π/6 (1/2)r²|₃^{1.5 + 3sin(θ)} dθ =

(1/2)∫_π/6^5π/6 (1.5 + 3sin(θ))² - 9 dθ =

(1/2) ∫_π/6^5π/6 (1.5 + 3sin(θ))² - 9 dθ =

(1/2) ∫_π/6^5π/6 (9/4 + 9sin(θ) + 9 sin²(θ) - 9 ) dθ =

(1/2) ∫_π/6^5π/6 (-27/4 + 9sin(θ) + 9 (1/2 - cos(2θ))) dθ =

(9/2) (- θ/4 - cos(θ) - (1/2) sin(2θ)) |_π/6^5π/6 =

(9/2) (- 5π/24 - cos(5π/6) - (1/2) sin(5π/3) + π/24 + cos(π/6) + (1/2) sin(π/3)) =

(9/2) (- 5π/24 - cos(5π/6) - (1/2) sin(5π/3) + π/24 + cos(π/6) + (1/2) sin(π/3))

= - π/6 + cos(π/6) - cos(5π/6) + (1/2) sin(π/3)) - (1/2) sin(5π/3) =

(9/2)( - π/6 + √3/2 + √3/2 + √3/4 + √3/4 ) =

(9/2)( - π/6 + √3 + √3/2 ) = (9/2)( - π/6 + 3√3/2) )

∫∫_D dA = - 3π/4 + 27√3/4