Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II: Volume of solid of revolution
In the area calculus section, we used definite integral
with two kinds of cut: the vertical slice and the horizontal slice.
In this section, we will use them determine the volume of
a solid of revolution.
If we rotate a solid object about a rotation axis,
each point of this solid makes a circular orbit around this axis.
To define the related generated volume we will use two
method: the disk method, and the cylindrical method.
In practise, the disk method is used with slices perpendicular
to the rotation axis and the cylindrical method is used with slices
parallel to the rotation axis.
1.Volume of solid of revolution
Disk method
1.1. Rotation axis is x-axis
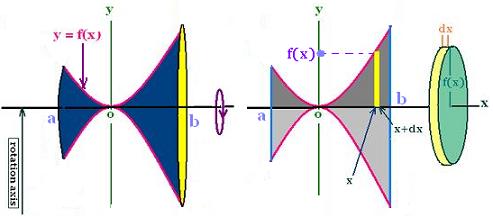
We want to determine the volume generated by the rotation
of the area delimited by the function f(x) and the rotation x-axis,
between the two bounds x = a and x = b.
Because we are using the disk method, let's cut slices perpenticular
to the rotation axis x-axis.
At the point x, the slice has f(x) as radius and dx as thickness.
So the area of the elementary disk at the point x is
disk(x) = π[f(x)]2.
The related elementary volume dV is
dV(x) = disk(x) dx = π[f(x)]2 dx .
The total volume generated by the complete rotation is
1.2. Shifted rotation axis
If the rotation axis is shifted by y = c around the
x-axis, we will have f(x) - c as the radius at the point x, so
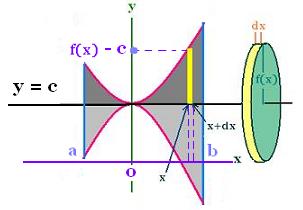
| |
b
| |
| V = ∫ | |
π [f(x) - c]2 dx
|
| |
a
| |
1.3. General case
Let f and g two functions continuous on the interval [a,b].
If within the whole interval [a, b], f(x) > g(x) > c, then the
volume of the solid of revolution generated by the rotation of
the area bounded by the curves of the two functions between x = a
and x = b about the c axis is:
| |
x = b
| |
| V = ∫ | |
π[(f(x) - c)2 - (g(x) - c)2]dx
|
| |
x = a
| |
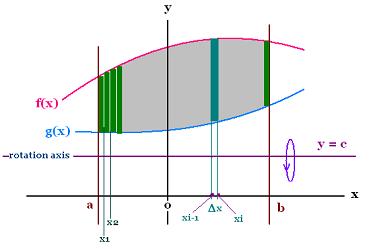
To determine the related volume, we will use Riemann sum integral
with vertical slices cut.
Let subdivise the interval [a, b] in n equal sub-intervals
of width Δx1, Δx2, Δx3, ... Δxn and take
the upper bound of each sub-interval as the representative.
In each subinterval, we construct a rectangle of width equal to
Δxi and height f(xi) - g(xi).
A complete rotation about c axis of all the n rectangles generates
a n washers. The volume of the ith washer is:
Vi = π[(f(xi) - c)2 - (g(xi) - c)2] Δxi
Therefore the sum of all these washers gives the
related volume.
| | |
i = n
| |
| V = lim | Σ | |
Vi
|
| n →+∞ | |
i = 1
| |
| |
x = b
| |
| V = ∫ | |
π[(f(x) - c)2 - (g(x) - c)2]dx
|
| |
x = a
| |
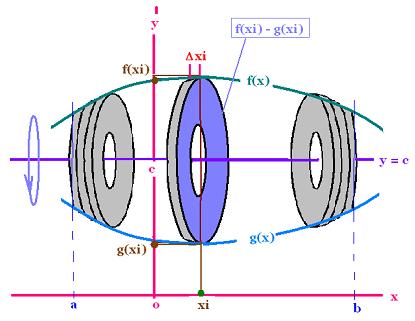
1.4. Examples
1.4.1. Example 1
Generated volume by the rotation of the area bounded
by the two curves of f(x) = x2 and g(x) = 0
between 0 and x = 1 around x = c = 0
We have: g(x) = c = 0, so
| |
x = 3
| |
| V = ∫ | |
π[(f(x))2]dx = πx4dx
|
| |
x = 0
| |
=
1.4.2. Example 2
Generated volume by the rotation of the area bounded
by the two curves of f(x) = x2 and g(x) = 0
between 0 and x = 1 around x = c = 1
We have: g(x) = 0, so
| |
x = 1
| |
| V = ∫ | |
π[(c - g(x))2 - (c - f(x))2]dx
|
| |
x = 0
| |
=
| |
x = 1
| |
| ∫ | |
π[(1 - 0)2 - (1 - f(x))2]dx
|
| |
x = 0
| |
=
| |
x = 1
| |
| ∫ | |
π[1 - (1 - x2)2]dx
|
| |
x = 0
| |
=
| |
1
| |
| π[2x3/3 - x5/5] | = 7π/15 |
|
| |
0
| |
1.4.3. Example 3
Generated volume by the rotation of the area bounded
by the two curves of f(y) = √y and g(y) = 1
between 0 and 1 = 1 around y = c = 10
We have:
f(y) = x = √ y;
g(y) = 0, so
| |
y = 1
| |
| V = ∫ | |
π[(f(y) - c)2 - ( g(y) - c)2]dy
|
| |
y = 0
| |
=
| |
y = 1
| |
| V = ∫ | |
π[(√y - 0)2 - ( 0 - 0)2]dy
|
| |
y = 0
| |
=
=
1.4.4. Example 4
f(x) = x2 between 0 and x = 1 around c = y = 1
Generated volume by the rotation of the area bounded
by the two curves of f(y) = √y and g(y) = 1
between 0 and 1 = 1 around y = c = 1
We have:
f(y) = x = √ y;
g(y) = c = 1, so
| |
y = 1
| |
| V = ∫ | |
π[(c - f(y) )2 - (c - g(y))2]dy
|
| |
y = 0
| |
=
| |
y = 1
| |
| V = ∫ | |
π[(1 - √y)2 - ( 0 - 0)2]dy
|
| |
y = 0
| |
=
| |
y = 1
| |
| V = ∫ | |
π[1 - 2√y + y]dy
|
| |
y = 0
| |
=
| |
1
| |
| π [y - (4/3)y3/2 + y2/2] | = π/6 |
|
| |
0
| |
2.Volume of solid of revolution
Cylindrical method
Let f and g two continuous functions on the interval [a,b].
If within the whole interval [a, b], f(x) >= g(x), then the
volume of the solid of revolution generated by the rotation of
the area bounded by the curves of the two functions between x = a
and x = b about the c axis with a >= c is:
| |
x = b
| |
| V = ∫ | |
2π(x - c)(f(x) - g(x)) dx
|
| |
x = a
| |
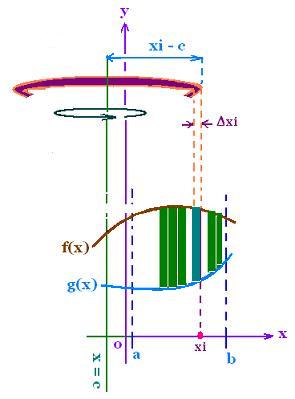
We want to determine the volume generated by the rotation
of the area delimited by the functions f(x) and g(x) about c-axis,
between the two bounds x = a and x = b.
Because we are using the cylinder method, let's cut shells parallel
to the rotation axis c-axis.
At the point xi, the shell has xi - c as radius (c<0)
and Δxi as thickness.
So the area of the elementary rectangle side at the point xi is
shell(xi) = height x Δxi = [f(xi) - g(xi)]Δxi.
The elementary volume dV of this shell
dVi = dV(xi) = shell(x) . 2π[xi - c] =
2π[xi - c] [f(xi) - g(xi)]Δxi.
The total volume generated by the complete rotation is
| | |
i = n
| |
| V = lim | Σ | |
Vi
|
| n →+∞ | |
i = 1
| |
=
| |
x = b
| |
| ∫ | |
2π[x - c] [f(x) - g(x)] dx
|
| |
x = a
| |
5. Exercises
|
|




