Calculus II: The derivative : applications
Theorems of analysis for the continuous functions

Computation of derivatives is useful to define some properties of related functions. The applications of derivatives are not just limited to information about graphs of functions and optimization problems, we use them also to set theorems of analysis for the continuous functions, and compute some particular limits.

1. Relative and absolute extrema of functions

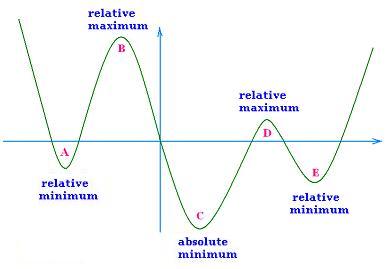
The term relative extrema of a function refers to the maximum and minimum of a function on a particular given region of the domain of the function, while the term absolute extrema refers to the maximum and the minimum of a function on its whole domain.

In the graph above, we have three minima :
- Two relative minima (A) and (E), and
- An absolute minimum (C).

- Two relative maxima (B) and (B), and
- No absolute maxima

2. Extreme Value Theorem

2.1. Definition:

A function f(x) that is continuous on the interval [a,b] has an absolute maximum and an absolute minimum within this interval. The reciprocal proposition is not true.

Every time we restrict the domain of a function to a closed interval (that contains end points), we get absolute maximums and absolute minimums.

2.2. Examples

1. f(x) = 1/x on [- 2, + 2]

This function is not continuous on the interval. So this theorem does not hold. We have no extrema in this interval.

2.





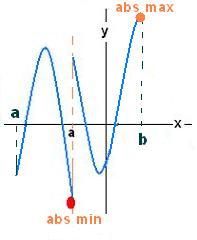
The graphed function is not continuous on the interval [a, b] and yet has absolute extrema; that means the reciprocal proposition is not true.

3. Critical points

3.1. Definition:

A real "c" is called a critical point of the function f(x) if f(c) exists and if f'(c) = 0 or doesn't exist.

3.2 Examples:

1. f(x) = x² - 2x

In order to find the critical points, we need the derivative of the function f(x).

f'(x) = 2 x - 2

The critical point of f is: (1, -1)

2. f(x) = x^1/2 + 1
f(0) exists.
f'(x) = (1/2) x^-1/2

f'(0) doesn't exist, so the point (0,1) is a critical point of the function f.

4. Critical value theorem (Fermat’s Theorem)

4.1. Definition:

If a function f(x) has a relative extrema at x = c and f'(c) exists, then x = c is a critical point of the function f(x).

In other terms, if a function f(x) has a relative extrema at x = c and f'(c) exists, then f'(c) = 0.

To give a proof, we assume that f(x) has a relative maximum (the related proof for a relative minimum is identical and obtained by just switching inequalities).

So, if f(x) has a relative maximum at x = c then f(x) >= f(c) for all x that are sufficiently close to c. That is f(x) >= f(c + h) for all h that are sufficiently close to zero (positive or negative).

f(x) >= f(c + h) is written as:
f(c + h) - f(x) <= 0
Dividing by h (> 0) gives:

(f(c + h) - f(x))/h <= 0

Taking the limits gives:

lim (f(c + h) - f(x))/h <= 0
h → 0⁺

As the limit is supposed exists, we have:

lim (f(c+h) - f(x))/h	= lim (f(c+h) - f(x))/h
h → 0+	h → 0-

= lim (f(c+h) - f(x))/h <= 0
h → 0

That is f'(c) <= 0

Now, for h < 0, we have
(f(c + h) - f(x))/h >= 0

Taking the limits gives:

lim (f(c + h) - f(x))/h >= 0
h → 0^-

As the limit is supposer exists, we have

lim (f(c + h) - f(x))/h =	lim (f(c + h) - f(x))/h
h → 0-	h → 0-

= lim (f(c + h) - f(x))/h >= 0
h → 0

That is f'(c) >= 0

Therefore, at the same time f'(c) <= 0, and f'(c) >= 0 , that is f'(c) = 0, which means x = c is a critical point.

4.2. Examples:

If a function f(x) has a relative extrema at x = c and f'(c) exists, then x = c is a critical point of the function f(x).

f(x) = - 2 x² + 18 has a relative extremum at x = 0.

f'(x) = - 4 x , f'(0) = 0 exists then x = 0 is a critical point of the function.

5. Rolle's Theorem

5.1. Definition:

If f(x) a function that satisfies the three following conditions:

1. f(x) is continuous on the closed interval [a,b].
2. f(x) is differentiable on the open interval ]a,b[.
3. f(a) = f(b)

Then it exists a number c such that a < c < b and f '(c) = 0.
That is f(x) has a critical (c, f(c)) in the interval ]a, b[.

To prove this theorem, we consider three cases:

1.f(x) is constant on [a,b] that is f(x) = k. So f'(x) = 0 for all x in the interval [a, b]. Then any x in this interval can be the expected real c., with f'(c) = 0

2 : f(x) is decreasing toward the final point (b,f(b)). Then there is some number d in ]a,b[ such that f(d) > f(b). Since f(a) = f(b) we have also f(d) > f(b).

By the first hypothesis , f(x) is continuous and we must have a relative maximum at a point c in the interval ]a, b[: a < x < b.

By the second hypothesis, f'(x) exists on ]a, b[, so f'(c) exists, and according to Fermat's theorem, c is a critical point. Hence f'(c) = 0.

3 : f(x) is increasing toward the final point (b,f(b)). Then there is some number d in ]a,b[ such that f(d) < f(b). Since f(a) = f(b) we have also f(d) < f(b).

By the first hypothesis , f(x) is continuous and we must have a relative minimum at a point c in the interval ]a, b[: a < x < b.

By the second hypothesis, f'(x) exists om ]a, b[, so f'(c) exists, and according to Fermat's theorem, c is a critical point. Hence f'(c) = 0.

5.2. Examples:

1.


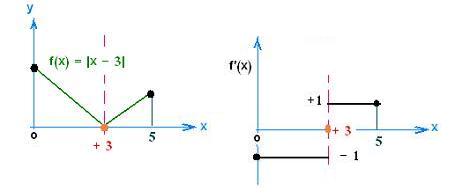
f(x) = |x - 3| =
x - 3 if x > 3
- x + 3 if x < 3

The function f(x) is continuous on the interval [0, 5]. Is it differentiable ?

f'(x) =
+ 1 if x > 3
- 1 if x < 3

lim f '(x) = + 1
x → 3⁺

lim f '(x) = -1
x → 3^-

lim f '(x) â‰	lim f '(x)
x → 3+	x → 3-

Therefore f'(x) does not exist.

The function f(x) = |x - 3| is not differentiable at the point (3,0).

So the Rolle's theorem does not apply.


2. f(x) = cos (x) on [0, 2Ï€]

The function f(x) is continuous on the interval [0, 2Ï€] and differentiable on ]0, 2Ï€[.

Since f(0) = f(2Ï€). The Rolle's theorem applies. It exists at least a real number c in ]0, 2Ï€[. such that f'(c) = 0.

3. f(x) = 3/(x + 2) on [-2, 4]

The function f(x) is not continuous at the point x = - 2, so the Rolle's theorem does not apply.

6. The Mean Value Theorem
(Lagrange's theorem)

6.1. Definition:

Let f(x) a function that satisfies the two following conditions:

1. f(x) is continuous on the closed interval [a,b].
2. f(x) is differentiable on the open interval ]a,b[.

Then there is a number c such that a < c < b and
f'(c) = (f(b) - f(a))/(b - a)


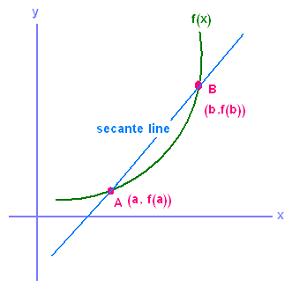
The equation of the secant going through the two points A nd B is written as:
y = m x + k ; m is the slope and k is the y-intercept.

By taking any point (x, y) in the secant line, the slope of this line is written as:

m = (y - f(a))/(x - a) = (f(b) - f(a))/(b - a)

That is:

y = f(a) + (f(b) - f(a))(x - a)/(b - a)

Let's define a new function g(x) equal to the difference between the function f(x) and the equation of the secant line y :

g(x) = f(x) - y = f(x) - [ f(a) + (f(b) - f(a))(x - a)/(b - a)]
= f(x) - f(a) - (f(b) - f(a))(x - a)/(b - a)

g(x) is the sum of:
- The function f(x) supposed continuous on [a, b] and differentiable on ]a, b[, and
- A linear polynomial (of the form "px + q") which is continuous and differentiable on R.

Therefore g(x) is continuous on [a, b] and differentiable on ]a, b[.

Computing the derivative of g(x) yields:
g'(x) = f'(x) - (f(b) - f(a))/(b - a)

We have assumed that f(x) is differentiable on the open interval ]a,b[. Then f'(x) exists. Since the last term - (f(b) - f(a))/(b - a) is just a constant, then g'(x) exists.

In addition we have

g(a) = f(a) - f(a) - (f(b) - f(a))(a - a)/(b - a)] = 0,
g(b) = f(b) - f(a) - (f(b) - f(a))(b - a)/(b - a)] = 0

The function g(x) satisfies then the three conditions of Rolle's theorem, Therefore, It exists a number c such as a <c < b, and g'(c) = 0.

That is g'(c) = f'(c) - (f(b) - f(a))/(b - a) = 0 , or

f'(c) = (f(b) - f(a))/(b - a)

6.2. Examples:

6.2.1. Example 1:

Let consider a function f(x) = x³ + 2 x² + 8 on the interval [1, 2].

This function is continuous and differentiable on the related interval. The Lagrange's conditions are satisfied.

f(1) = 11
f(2) = 24

(f(2) - f(1))/(2 - 1) = 13

f '(x) = 3 x² + 4 x

f '(c) = 3 c² + 4 c that shall be equal to 13. Therefore

3 c² + 4 c - 13 = 0

Δ' = 4 - (3)(- 13) = 43

We find two points:

c1 = - (2 + √43)/3 = - 2.85
c1 = - (2 - √43)/3 = + 1.52

Only c1 = - (2 - √43)/3 = + 1.52 is retained.

6.2.2. Example 2:

A car starts from rest and travels 100 m in 10 s. Its average speed, during the interval of 10 seconds is the 100/10 = 10 m/s.

1. How many times the speedometer must indicate exactly the value 10 m/s ?

This speed of 10 m/s could be achieved at least once according to the mean value theorem.

2. If the car reaches the speed of 90 km/h at the end of the interval of 10 seconds, show that at some point, the acceleration of the car was exactly 2.5 m/s².

Let f the speed function of time f(t), then

(s(10) - s(0))/(10 - 0) = (90 - 0)/10 = 9 km/h/s = 2.5 m/s²

According to Lagrange's theorem, the car must reaches the acceleration of 2.5 m/s² at least once.

7. The Generalized Mean Value Theorem
(Cauchy's theorem)

7.1. Definition:

If f(x) and g(x) two functions that satisfies the two following conditions:

1. f(x) is continuous on the closed interval [a,b].
2. f(x) is differentiable on the open interval ]a,b[.
3. g(x) ≠ 0 on the open interval ]a,b[.

Then there is a number c such that a < c < b and (f(b) - f(a))/(g(b) - g(a)) = f'(c)/g'(c)

Proof:



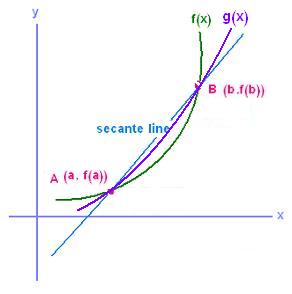
We define a new function h(x) as we did earlier such that:

h(x) = f(x) - [ f(a) + (f(b) - f(a))(x - a)/(b - a)]
= f(x) - f(a) - (f(b) - f(a))(x - a)/(b - a)

For the function g(x), we have the slope:
(g(x) - g(a))/(x - a) = (g(b) - g(a))/(b - a)
or
(x - a) /(b - a) = (g(x) - g(a))/ (g(b) - g(a))

Substituting this relationship in the expression of h(x), we find:

h(x) = f(x) - f(a) - (f(b) - f(a))(g(x) - g(a))/(g(b) - g(a))

Since, by hypothesis, f(x) and g(x) are continuous on the interval [a, b] and differentiable on ]a, b[, so does the function h(x).

We have also:

h(a) = f(a) - f(a) - (f(b) - f(a))(g(a) - g(a))/(g(b) - g(a)) = 0

h(b) = f(b) - f(a) - (f(b) - f(a))(g(b) - g(a))/(g(b) - g(a)) = 0
Hence the Rolle's theorem holds.

The derivative of h(x) yields:

h'(x) = f'(x) - (f(b) - f(a))(g'(x))/(g(b) - g(a))

According to the Rolle's theorem , there exists a real c such as h'(c) = 0.

So

f'(c) - (f(b) - f(a))(g'(c))/(g(b) - g(a)) = 0

That is

(f(b) - f(a))/(g(b) - g(a)) = f'(c)/(g'(c))

Note:
g'(c) ≠ 0 because g(x) ≠ 0 on ]a, b[ by hypothesis, and
(g(b) - g(a)) ≠ 0 otherwise, according to the Rolle's theorem, there will exist a real xo such that g'(xo) = 0 which contradicts the hypothesis of the theorem.

7.2. Examples:

8. Intermediate Value Theorem

8.1. Definition:

Let f (x) be a continuous function on the interval [a, b]. If d [f (a), f (b)], then there is a c [a, b] such that f (c) = d

8.2.Example:

Show that the polynomial P(x) = x² - x - 2 has a root somewhere in the interval[0,3].

Solution

In other words, we want to show that if 0 [P(0), P(3)], then there is a c [0, 3] such that P(c) = 0.

To prove that root exit, we use the Intermediate Value Theorem.

The function P(x) is continuous in [0,3] as the polynomial is continuous everywhere.

P(0) = - 2 ≤ d = f(c) ≤ P(3) = 4

Therefore by the Intermediate Value Theorem, there must be a number c between 0 and 3 so that P(x) = 0.

Therefore the polynomial does have a root between 0 and 3.