Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II: Area integrals
If we rotate a solid object about a rotation axis,
each point of this solid makes a circlar orbit around this axis.
To define the related generated volume we will use definite
integrales. There are two ways to evaluate this volume, the first
method uses vertical slices, the second uses horizontal
slices. In pratique, we use the vertical slices perpendicular to the
rotation axis
1.Area between two curves
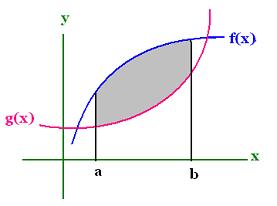
Let two functions f(x) and g(x) continuous in the interval [a, b],
with f(x) >= g(x) for all values in this interval [a, b].
The area bounded by the related two curves between
a and b is:
2. Example 1
2.1. Example 1
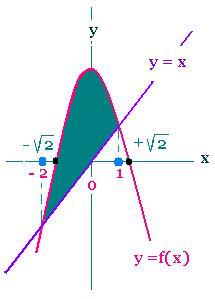
What is the value of the area between the two curves of
the two functions f(x) = - x2 + 2 and the function g(x) =
x from 0 to x = 1 ?
| | 1 | |
| [- x3/3 - x2/2 + 2x ] | = 7/6 |
| | 0 | |
2.2. Example 2
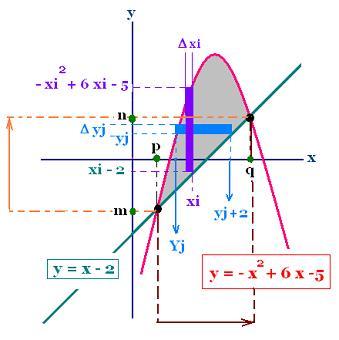
2.2.1. Vertical slices (vertical strips)
The points p and q are given by the intersection
of the two curves, so
- x2 + 6x - 5 = x - 2
That gives:
p = (5 - √13)/2
q = (5 + √13)/2
h(x) = [- x2 + 6x - 5] - [x - 2] =
- x2 + 6x - 5 - x + 2 = - x2 + 5x - 3
| |
q = (5 + √13)/2
| |
| ∫ | |
h(x) dx
|
| |
p = (5 - √13)/2
| |
=
| |
q
| |
| [- x3/3 + 5x2/2 - 3 x ] | |
|
| |
p
| |
2.2.1. Horizontal slices
y = - x2 + 6x - 5
x2 - 6x + 5 + y = 0
The expression of x with respect to y is:
y1 = 3 - [4 - y]1/2 always < 0
y2 = 3 + [4 - y]1/2 always > 0
The definite integrale goes from m to 0 then
from o to n
n = q - 2 = (5 + √13)/2 - 2 = (1 + √13)/2
m = p - 2 = (5 - √13)/2 - 2 = (1 - √13)/2
h(y) = h1(y) + h2(y)
h1(y) = (y + 2) - y1 = (y + 2) - (3 - [4 - y]1/2)
h1(y) = y - 1 + [4 - y]1/2) for y < 0
h2(y) = (y + 2) - y2 = (y + 2) - (3 + [4 - y]1/2)
h2(x) = y - 1 - [4 - y]1/2) for y > 0
| |
n
| | |
|
0
| |
|
|
n
| |
| ∫ | |
h(y) dy
| = |
∫ | |
h1(y) dy +
|
|
∫ | |
h2(y) dy
|
| |
m
| | |
|
m
| |
|
|
0
| |
We have:
| |
| |
| ∫ | |
h1(y) dy = y2/2 - y - (2/3)(4 - y)3/2 = H1(y)
|
| |
| |
and
| |
| |
| ∫ | |
h2(y) dy = y2/2 - y + (2/3)(4 - y)3/2 = H2(y)
|
| |
| |
Therefore
| |
n
| |
| ∫ | |
h(y) dy = H1(0) - H1(m) + H2(n) - H2(0)
|
| |
m
| |
H1(0) = - 16/3
H2(0) = 16/3
n = (1 + √13)/2
m = (1 - √13)/2
H1(y) = y2/2 - y - (2/3)(4 - y)3/2
H2(y) = y2/2 - y + (2/3)(4 - y)3/2
5. Exercises
|
|