Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II: Arc length
We know how to calculate the length of some regular
curves such as a line, circle. Using the Riemann sum,
then the definite integral, we can calculate the
length of any curve under certain conditions.
1.Length of an arc of a curve
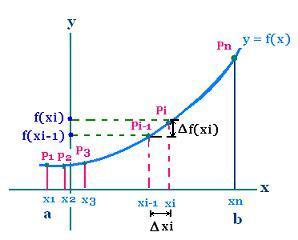
Let f(x) a continuous function on the interval [a, b] and
its derivative f'(x) is continuous in the interval ]a, b[.
We want to determine the length of the curve L of
the function f(x) from x = a to x = b.
Let subdivide the interval [a, b] in n equal sub-intervals
of width Δx1, Δx2, Δx3, ... Δxn.
In the ith sub-interval, the expression of the length of an elementary arc is dLi is:
dLi = [(f(xi) - f(xi - 1))2 + (xi - xi -1)2]1/2
The length of the total arc is:
| | |
i = n
| |
| L = lim | Σ | |
Li
|
| n →+∞ | |
i = 1
| |
=
| |
b
| |
| ∫ | |
[(df(x))2 + (dx)2]1/2
|
| |
a
| |
=
| |
b
| |
| ∫ | |
[(df(x)/dx)2 + 1]1/2 dx
|
| |
a
| |
=
| |
b
| |
| ∫ | |
[1 + (f '(x))2]1/2 dx
|
| |
a
| |
2.Examples
f(x) = [R2 - x2]1/2
from x = 0 to x = R.
f(x) is continuous on [- R, + R], so it does
on [0,R]
f '(x) = - x/ [R2 - x2]1/2
f '(x) is continuous on ]0,R[
| |
R
| |
| ∫ | |
[1 + (f '(x))2]1/2 dx
|
| |
0
| |
=
=
| |
R
| |
| ∫ | |
dx/[1 - (x/R)2]1/2 dx
|
| |
0
| |
= πR/2 , that is the quarter of a circle.
3. Exercises
|
|