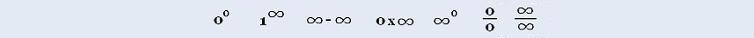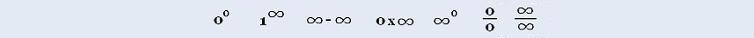Calculus I: Limits
The concept of limit

1. Limits: Intuitive approach and definitions

Using a calculator

Let a function f defined as

f(x) = 2 x + 3

We want to study the behavior of the images of this function for the values of x close to the value 1.

We have the following two cases:

x approaches 1 from the left:

x → 1	f(x)
0.5	4.0
0.77	4.54
0.85	4.70
0.955	4.91
0.999	4.998

As the variable x takes values close to 1 (while remaining less than 1), the related images of the function f approach the value 5.

We say that when the value of variable x approaches 1 by the left, the images become close to the value 5.

In a more concise manner, we write:

lim f(x) = 5
x → 1^-

x approaches 1 from the right:

1 ← x	f(x)
1.75	6.50
1.50	6.00
1.2	5.40
1.05	5.10
1.005	5.01

Similarly, the more the variable x takes values close to 1 (while remaining greater than 1), the more the related images of the function f approach the value 5.

We say that when the value of the variable x approaches 1 from the right, the function takes values close to the value 5.

In a more concise, we write:

lim f(x) = 5
x → 1⁺

We have:

lim f(x) = x → 1-

lim f(x) = 5 x → 1+

Where in both cases, the value obtained is the same, we write:

lim f(x) = 5
x → 1

Therefore:

 

lim f(x) = b x → a

if and only if

lim f(x) = b x → a- and lim f(x) = b x → a+

a and b are real.

Recall then:

a) If

lim f(x) ≠ x → a-

lim f(x) x → a+

Then
lim f(x) does not exist.
x → a

b) If

lim f(x) doesn't exist OR x → a-

lim f(x) doesn't exist x → a+

Then
lim f(x) does not exist.
x → a

2. Examples

2.1. Example 1

Let f a function defined as:

f(x) = (√x - 2)/(x - 4)

We want to know the following;

a)
lim f(x)
x → 4

b) lim f(x)
x → 0

c) lim f(x)
x → 1

d) lim f(x)
x → +∞

a)
lim f(x)
x → 4^-

x → 4	f(x)
3.05	0.26
3.40	0.26
3.0	0.26
3.80	0.253
3.998	0.250

lim f(x)
x → 4⁺

4 ← x	f(x)
5	0.236
4.75	0.239
4.20	0.247
4.01	0.249
4.005	0.250

We have then:

lim f(x) = 0.25
x → 4^-
lim f(x) = 0.25
x → 4⁺
So
lim f(x) = 0.25
x → 4

b)
lim f(x) doesn't exist
x → 0^-

lim f(x) = 5
x → 0⁺
so
lim f(x) doesn't exist.
x → 0

c)

lim f(x) = x → 1-

lim f(x) = 1/3 x → 1+

so
lim f(x) = 1/3
x → 1

d) lim f(x) = 1/2
x → +∞

2.2. Example 2

f(x) = (x² - 9)/(x - 3)

lim f(x) = x → 3-

lim (x + 3) = 6 x → 3-

lim f(x) = x → 3+

lim (x + 3) = 6 x → 3+

Therefore:

lim f(x) = 6
x → 3

3. Exercises

3.1 Graph the following functions and use those graphs to
determine the related limits:

a)
f(x) = 2/(x - 3)

lim f(x)
x → 3⁺

lim f(x)
x → 3^-

lim f(x)
x → 3

b)
f(x) = (x² - 16)/(x + 4)

lim f(x)
x → 4⁺

lim f(x)
x → 4^-

lim f(x)
x → 4

3.2. Determine the following limits:

c)
f(x) = (2 - x)^1/2

lim f(x)
x → 2⁺

lim f(x)
x → 2^-

lim f(x)
x → 2

d)
f(x) = |x - 7| - 1

lim f(x)
x → 7⁺

lim f(x) x → 7^-

lim f(x)
x → 7

e)
f(x) = x² - 1 if x > 0
f(x) = x + 1 if x < 0

lim f(x)
x → 0⁺

lim f(x)
x → 0^-

lim f(x)
x → 0

3.3. For each of the graphed function, determine the following limits:



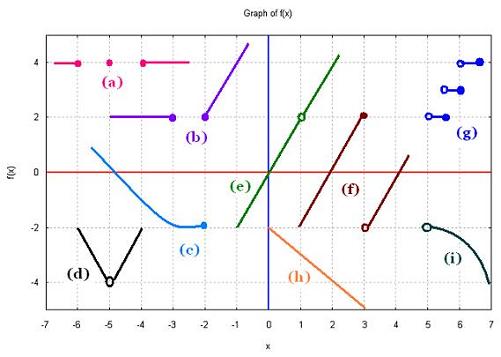
(a)
lim f(x)
x → - 5

(b)
lim f(x)
x → - 3

(c)
lim f(x)
x → - 2

(d)
lim f(x)
x → - 5

(e)
lim f(x)
x → + 1

(f)
lim f(x)
x → + 3

(g)
lim f(x)
x → + 5.25

(h)
lim f(x)
x → + 1

(i)
lim f(x)
x → + 5