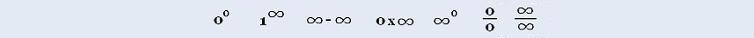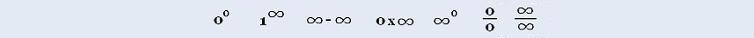Calculus I: exponential function
logarithmic function and derivative

1. Derivative: exponential functions

1.1. Definitions

1.1.1. Derivative of e^x

d/dx(e^x) = e^x

By definition,

d/dx(ex) =	lim( ex + Δx - ex)/Δx = 0/0 = Undetermined
	Δx → 0

= ex	lim (eΔx - 1)/Δx
	Δx → 0

We know :

lim (e^x - 1)/x = 1
x → 0

Therefore:
de^x/dx = e^x

1.1.2. Derivative of e^g(x)

let:
f(x) = y , and g(x) = u, so y = e^u.

According to the chain rule formula:

dy/dx = (dy/du).(du/dx)
= e^u . d/dx(g(x)) = e^u . g'(x) =
f(x) . g'(x) = e^g(x) . g'(x)

1.1.3. Derivative of b^g(x)

We make use of the change of base rule for the exponential function b^g(x):

(b^g(x) = e^{ln b g(x)}

d/dx (b^g(x)) = d/dx ( e^{ln bg(x)}) =
d/dx (e^{ln b . g(x)}) = d/dx (ln b . g(x)) . (e^{ln b . g(x)}) =
ln b . d/dx (g(x)) . (e^{ln b . g(x)}) = ln b . d/dx (g(x)) . (b^g(x)) =

Therefore:

d/dx (b^g(x)) = ln b . d/dx (g(x)) . (b^g(x))

1.2. Examples

a) f(x) = e^4x
f'(x) = (4x)'. e^4x = 4 e^{4 x}

b) f(x) = 3x e^x2
f'(x) = (3x)' e^x2 + 3x (e^x2)' = 3 e^x2 + 3x ((x²)' e^x2) =
= 3 e^x2 + 3x (2 x e^x2) = = 3 e^x2 + 6 x² e^x2 = = e^x2 (3 + 6 x²)

c) f(x) = 2^3x
d(2^3x)/dx = ln 2 . 3. 2^3x = 3 (ln 2) 2^3x

d) f(x) = (1/2)^{x + 4} = - (ln 2) (1/2)^{x + 4}

2. Derivative: logarithmic functions

2.1. Definitions

2.1.1. Derivative of ln(x)

Let y = ln(x) then e^y = x . So
d/dx(e^y) = d/dx(x) = 1
dy/dx . (e^y) = d/dx(x) = 1

Therefore:
dy/dx = 1/e^y = 1/x

Hence:
d ln(x) /dx = 1/x

2.1.2. Derivative of ln g(x)

Let y = ln u with g(x) = u
Using the chain rule for derivative, we have:

dy/dx = (dy/du).(du/dx) = (1/u).(du/dx) = (1/g(x)).(dg(x)/dx)

Therefore:

d ln(g(x))/dx = (1/g(x)).(dg(x)/dx)

2.1.3. Derivative of log_bg(x)

We make use of the change of base for
the logarithmic function log_bg(x):

log_bg(x) = log_eg(x) / log_eb = ln g(x)/ ln b

d/dx[log_bg(x)] = d/dx[ln g(x)/ ln b] =
(1/ln b) . d/dx[ln g(x)] = (1/ln b) . d/dx[g(x)] /g(x)

Therefore:

d/dx[log_bg(x)] = (1/ln b) . d/dx(g(x)) /g(x)

2.1.4. Logarithmic derivatives

Logarithmic derivative is used when the derivative of some functions is so long or so complicated to perform. These functions generally include products, ratios, or exponents. This technique do the job very quickly.

Let y = f(x). f(x) is the "complicated" function.

The method is then:

1. Take the ln of both sides:
2. ln y = ln f(x)
3. Set the derivative of both sides:
4. (1/y).dy/dx = f'(x)/f(x)
5. Once f'(x)/f(x) is solved, we write the expression of dy/dx.
6. dy/dx = y [f'(x)/f(x)]

The logarithmic derivative is used also to differentiate expressions of the form:
y = f(x)^g(x)

That is when the base of the exponantial f(x) and the exponent g(x) depend on the independent variable x.
In the general case where y = u^v, the logarithmic derivative gives:
ln y = v ln u , so
(1/y)dy/dx = (dv/dx) ln u + v (1/u)(du/dx)

Therefore:

dy/dx = y[(dv/dx) ln u + v (1/u)(du/dx)] = u^v[(dv/dx) ln u + v (1/u)(du/dx)] =
u^v (dv/dx) ln u + v u^{v - 1}(du/dx)

Hence:

The derivative of y = u^v is:
dy/dx = u^v (dv/dx) ln u + v u^{v - 1}(du/dx)

2.1.5. Absolute value: logarithmic derivatives

Using the relationship:

d ln(f(x))/dx = (1/f(x)).(df(x)/dx) = f'(x)/f(x)

We write:

d ln |f(x)|/dx =

d ln f(x)/dx = (1/f(x)).(df(x)/dx) =
f'(x)/f(x) if f(x) > 0

= d ln (- f(x))/dx = (1/(- f(x))).(df(x)/dx) =
f'(x)/f(x) if f(x) < 0

In both case, the result is f'(x)/f(x).

Therefore:

d ln |f(x)|/dx = (1/f(x)).(d f(x)/dx) = f'(x)/f(x)

Now, we want to derive an absolute value: y = |f(x)|

We have:

dy/dx =

d f(x)/dx if f(x) > 0
- d f(x)/dx if f(x) < 0

Using the logarithmic derivative, we have:

ln y = ln |f(x)|. So

(1/y)(dy/dx) = f'(x)/f(x)

dy/dx = y . f'(x)/f(x)

That is:

d|f(x)|/dx = |f(x)|. f'(x)/f(x)

2.2. Examples

a)
f(x) = ln(x) /x
f'(x) = (x ln'(x) - (x)' ln (x))/x² = (x (1/x) - 1. ln (x))/x² =
(1 - ln (x))/x²

b)
f(x) = ln (2 x + 3)
f'(x) = (2 x + 3)'/(2 x + 3) = 2/(2 x + 3)

c)
f(x) = log₃ (2 x + 1)
f'(x) = (1/ln 3) . (2 x + 3)'/(2 x + 3) = (2/ln 3)/(2 x + 3)

d)
f(x) = log (x)
f'(x) = (1/ln 10) . (x)'/x = (1/ln 10)/x

e)
f(x) = x² (x + 1)²/(x³ + 1)

y = f(x)
ln y = ln f(x) = ln [x² (x + 1)²/(x³ + 1)] =
ln x² + ln (x + 1)² - ln (x³ + 1) =
2 ln x + 2 ln (x + 1) - ln (x³ + 1)

Taking the derivatives yields:

(1/y)dy/dx = 2 (1/x) + 2. 1/(x + 1) - (3x²)/(x³ + 1) =
2/x + 2/(x + 1) - 3x²/(x³ + 1)

Then:

dy/dx = y [2/x + 2/(x + 1) - 3x²/(x³ + 1)] =
x² (x + 1)²/(x³ + 1) . [2/x + 2/(x + 1) - 3x²/(x³ + 1)]

Therefore:

dy/dx = x² (x + 1)²/(x³ + 1) . [2/x + 2/(x + 1) - 3x²/(x³ + 1)]

Expression that can be reduced.

f)
f(x) = |2 x - 1|
ln f(x) = ln |2 x - 1|
d ln f(x)/dx = d ln |2 x - 1|/dx = d ln |2 x - 1|/dx = d ln (2 x - 1)/dx = 2/(2 x - 1)

g)
y = |4x - 5|
ln y = ln |4x - 5|. So
(1/y)(dy/dx) = 4/(4 x - 5)
d|4x - 5|/dx = 4 |4x - 5|/(4x - 5)

3. Exercises