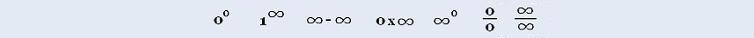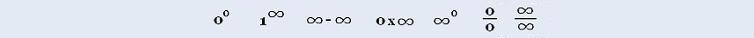Calculus: Derivative of a function

1. Definition of the derivative a function f

The derivative of a function y = f(x) denoted by dy/dx is :

dy/dx = df(x)/dx =

lim Δy/Δx Δ x → 0

= lim (f(x + Δ x) - f (x))/Δ x Δ x → 0

when this limit exists in R.

When the limit exists, the function is differentiable at x. If it is differentiable for all values of its domain, we say simply that the function is differentiable.

We use also the notations y' or f'(x) for the derivative of the function f.

2. Derivative a function f at a point x = a

The derivative a function f at a point x = a is denoted by

f'(a) = dy/dx |x = a

= lim (f(x) - f(a))/(x - a) Δ x → a

when this limit exists in R.

The derivative is interpreted as the instantaneous rate of change of the function for a given value of x. From a geometric point of view, the derivative of a function is the slope of the line tangent to the curve of the function to a given value of x.

3. Example

What is the derivative of the function
f(x) = 2 x² - 1
at
a) a = 1
b) a = 4 ?

f'(a) = df(x)/dx |_{x = a}
= lim (f(x) - f(a))/(x - a)
x → a
= lim ((2 x² - 1)- (2 a² - 1))/(x - a)
x → a
= lim (2 x² - 1 - 2 a² + 1)/(x - a)
x → a
= lim 2( x² - a² )/(x - a)
x → a
= lim 2(x + a) = 4 a
x → a

a) At a = 1, we have:
f'(1) = 4 . 1 = 4

b) At a = 4, we have:
f'(4) = 4 . 4 = 16

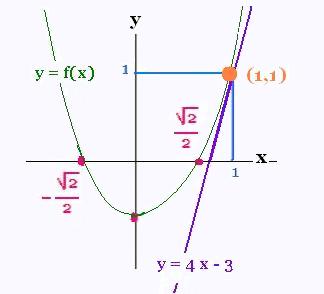
The point a = 1 has f(1) = 2 . 1² - 1 = 2 - 1 = 1 So the point (1,1) is a point on the curve.

The derivative of the function f at the point x = 1 is f'(1) = 4 which is the slope of the line tangent to the curve of f at the point (1,1).

Therefore, we can write the equation of the line tangent to the curve of f at the point (x,y) :

y = f'(1) x + b = 4. x + b = x + b

As the point (1,1) is on the curve, we write:
1 = 4.1 + b, so b = - 3 . The equation of the line tangent to the curve of f at the point (1,1) is :

y = 4 x - 3



a) At the point a = 4
f(4) = 2 . 4² - 1 = 31
f'(4) = 16

so
The equation of the line tangent to the curve of f at the point (4,31) is :
y = 16 x + b

As the point (4,31) is on the curve, we write:
31 = 16 . 4 + b

Then
b = 31 - 64 = - 33

Therefore:

y = 16 x - 33

4. Derivation and continuity of a function

If a function f is differentiable at x = a, then it is continuous at this point.

Proof:

f is differentiable at x = a. That is

f'(a) = lim (f(x) - f(a))/(x - a) = b
x → a

We can write:

lim (f(x) - f(a))
x → a
= lim (f(x) - f(a)) . lim (x - a)/(x - a)
x → a

= lim (f(x) - f(a))/(x - a) . x → a

lim (x - a) x → a

= b . 0 = 0

Then:

lim (f(x) - f(a)) = 0
x → a
or

lim f(x) x → a

= lim f(a) x → a

That is f is continuous at the point a.

The rule is:

If a function f is differentiable at x = a, then it is contineous at this point. But the converse is not true.

If f is discontiueous at a point then it is not differentiable at this point.

In general a function is not differentiable at a certain point if the function:
• is discontinuous at this point,
• has a vertical tangent at this point
(where the rate of change is infinite),
• has an angular point at this point.

5. Exercices: