La matrice est régulière: det (A) = 2 ≠ 0.
x = 2 et y = 3 est la solution, et cette solution est unique. 1.2.2. Exemple 2 : Système 3 x 3
On veut résoudre le système suivant par la méthode de la matrice inverse:
Sous forme matricielle A X = B ,
La matrice est régulière: det (A) = 4 ≠ 0.
x = - 2 et y = 3 et z = 1 est la solution, et cette solution est unique. 1.3. Règle de Cramer
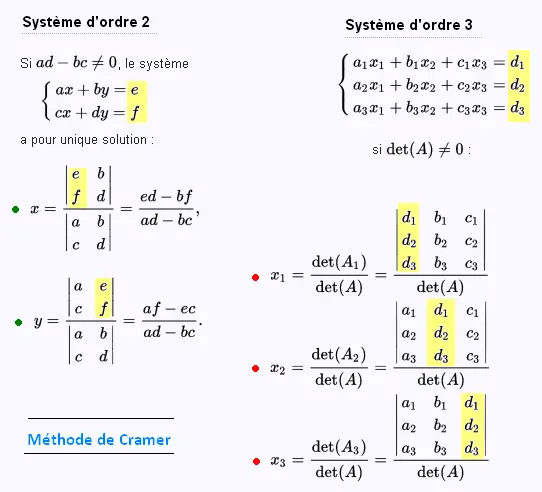
Pour résoudre un système de n équations linéaires à n inconnues
où la matrice des coefficients est régulière, on utise une méthode
simple dite règle de Cramer . cette méthode employe
juste des déterminants.
2. Systèmes de m équations à n inconnues
Les deux méthodes , celle de la matrice inverse et celle de
Cramer, utilisées ont des limites. Elle ne fonctionnent qu'à conditions
d'avoir le nombre d'équations est égal au nombre d'inconnues et si
la matrice des coefficients est régulière.
2.1. Méthode de la matrice escalier
À partir d'un système, on construit la matrice augmentée,
puis on effectue des transformations élémentaires sur les
LIGNES jusqu'à ce que l'on arrive à une matrice escalier
permettant de voir la solution.
La matrice augmentée est:
On en déduit facilement z = - 1 , y = 0 et , en remplaçant ces valeurs dan la première équation, on obtient x = 2. Le cheminement pour passer de la matrice augmentée à celle qui lui est équivalente n'est évidemment pas unique. Pour éviter d'augmenter inutilement le nombre d'étapes de cette méthode, on systématise la procédure à suivre en établissant la stratégie suivante: • Amener à 1 le premier élément de la première colonne, • Amener des 0 dans le reste de la première colonne, • Amener à 1 (ou à 0) le deuxième élément de la deuxième colonne, • Amener des 0 le reste de la deuxième colonne, • Poursuivre de la même manière avec les colonnes suivantes jusqu'à l'obtention de la matrice escalier. 2.2. Méthode d'élimination de Gauss-Jordan
La méthode d'élimination de Gauss-Jordan mène directement
à la solution.
La matrice augmentée est:
On effectuant les transformations élémentaires suivantes sur les lignes: L2 - 2L1, L3 - L1, (- 1/4)L2, L3 - 2L2, -2L3, on obtient la matrice escalier équivalente suivante:
On poursuit les transformations élémentaires sur les lignes: L1 - L2, L1 - (1/4)L3, et L2 - (3/4)L3. On obtient:
Cette matrice contient la sous-matrice identité I3, donc les solutions de X sont les élements de la matrice image B: x = 1, y = 2, et z = 3. 3. Systèmes inconsistants
Un système d'équations linéaires est inconsistant lorsqu'il
n'a pas de solutions.
La matrice augmentée est:
On effectuant les transformations élémentaires suivantes sur les lignes: L1 - L2, et L3 - L1, on obtient la matrice escalier équivalente suivante:
Sans continuer les transformations, la troisième ligne donne 0 = 6, ce qui est impossible. Le système n'a donc pas de solutions. Un tel système est dit inconsistant . 3. Systèmes consistants
Un système d'équations linéaires admet une infinité de solutions
lorsque le nombre de ses équations est inférieur au nombre d'inconnues.
La matrice augmentée est:
On effectuant les transformations élémentaires suivantes sur les lignes: L2 - 2L1, L3 - 3L1, et L3 - L2on obtient la matrice escalier équivalente suivante:
On complétant la résolution avec la méthode d'élimination de Gauss-Jordan: - (1/5)L2 , et L1 - 2L2, on obtient:
Ce qui mène au système de 2 équations à 3 inconnues suivant:
Ce système possède la solution : z = 0 , x = 8/5 , et y = 6/5, puis la solution x = 1, z = 1, y = 1 , puis ... Une infinité de solutions. On a donc au moins une solution, le système est dit consistant Toutes les solutions d'un tel système sont dites solutions particulères. Les solutions possibles sont alors obtenues en choisissant une inconnue comme paramètre, d'exprimer les autres en fonction de ce paramètre, puis de donner à celui-ci des valeures arbitraires. Ici par exemple, en choisissant z comme paramètre, on aura la solution complète en termes des constantes et du paramètre: x = (8/5) - (3/5) z y = (6/5) - (1/5) z Ce système d'équations linéaires admet une infinité de solutions puisque le nombre de ses équations est inférieur au nombre d'inconnues. La troisième éaquation du système initial n'est en fait que la somme de la première et de la deuxième équation. Cette troisième équation est donc inutile et n'apporte rien de nouveau pour la résolution du système. Dans toute situation similaire, les transformations élémentaires sur les lignes conduisent à une ligne de 0 l'équation inutile correspondante formé d'une combinaison linéaire des autres lignes du système. 4. Rang d'une matrice
On appelle rang d'une matrice l'ordre de sa plus grande
sous-matrice carrée régulière.
À partir de cette matrice 3 x 4, on tire la sous matrice 3 x 3 suivante en enlevant la dernière colonne:
Puisque son déterminant est égal à 7, ≠ 0, c'est donc la plus grande sous matrice carrée régulière qui peut venir de la matrice originale. Le rang de la matrice initiale est donc l'ordre de cette plus grande sous matrice carrée régulière , qui vaut 3. Si A est cette matrice initiale, on ecrit: rang(A) = 3 5. Theorème sur le rang d'une matrice5.1. Forme normale d'une matrice
Les transformations élémentaires faites sur une matrice ne changent
pas le rang de cette matrice.
Chacune de ces formes est une forme normale de la matrice. En réduisant une matrice à sa form normale, on obtient immédiatement le rang de la matrice. Exemple:
On effectuant les transformations élémentaires sur les colonnes: C2 + C1, C3 - 2C1, C4 - 3C1, (1/3)C2, (- 1)C3, C1 - 2C2, C4 + 3C2, C1 + (2/3)C3, C2 - (1/3)C3, C4 - 3C3, on obtient:
Cette dernière forme est la forme normale de la matrice originale. On en déduit immédiatement que le rang est 3. Le chemin emprunté pour réduire la matrice initiale à sa forme normale n'est pas unique. D'un point de vue stratégique, on essaie de réduire tous les éléments d'une ligne, ou d'une colonne à 0, sauf peut être un de ces éléments. Puis on répète le processus avec une autre rangée, et ainsi de suite. 5.2. Matrice escalier
On peut trouver le rang d'une matrice d'une manière systématique en
transformant cette matrice en une matrice escalier. Le rang est alors
déterminé par le nombre de lignes non nulles .
On effectuant les transformations élémentaires suivantes sur les lignes seulement : L2 - 2L1, L3 - 3L1, L4 - 5L1, L4 - L3, L3 - 4L2, (- 1/2)L2, (- 1/9)L3, on obtient la matrice escalier équivalente suivante:
Qui est une matrice escalier, avec 3 lignes non nulles. La sous-matrice triangulaire:
a un déterminant égal à 1, donc non nul. La matrice original A est donc de rang 3. rang(A) = 3 , qui est évidemment aussi le nombre de lignes non nulles de la matrice escalier. 5.3. Théorème
Si A X = B est un système d'équations linéaires, avec m équations et n inconnues,
dont la matrice des coefficients A est une matrice de format m x n et de rang p, et
si [A|B], la matrice augmentée du système, est de rang q, alors ce système:
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 B .
B .
